At what speed does a 1000 kg compact car have the same kinetic energy as a 20,000 kg truck going 25 km/h?

A mother has four times the mass of her young son. Both are running with the same kinetic energy. What is the ratio v_son/v_mother of their speeds?

A pitcher accelerates a 150 g baseball from rest to 35 m/s. How much work does the pitcher do on the ball?

The cable of a crane is lifting a 750 kg girder. The girder increases its speed from 0.25 m/s to 0.75 m/s in a distance of 3.5 m. How much work is done by gravity?

You throw a 5.5 g coin straight down at 4.0 m/s from a 35-m-high bridge. What is the speed of the coin just as it hits the water?

A 45 g bug is hovering in the air. A gust of wind exerts a force $\vec{F}=(4.0\hat{ı}-6.0\hat{ȷ})\times {10}^{-2}\text{N}$ on the bug. What is the bug's speed at the end of this displacement? Assume that the speed is due entirely to the wind.

A 25 kg air compressor is dragged up a rough incline from ${\vec{r}}_1=(1.3\hat{ı}+1.3\hat{ȷ})\text{m}$ to ${\vec{r}}_2=(8.3\hat{ı}+2.9\hat{ȷ})\text{m}$, to where the y-axis is vertical. How much work does gravity do on the compressor during this displacement?

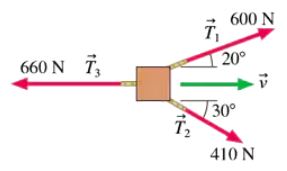
The three ropes shown in the bird's-eye view of FIGURE EX9.18 are used to drag a crate 3.0 m across the floor. How much work is done by each of the three forces?

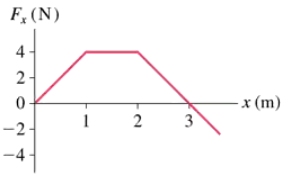
FIGURE EX9.20 is the force-versus-position graph for a particle moving along the x-axis. Determine the work done on the particle during each of the three intervals 0–1 m, 1–2 m, and 2–3 m.

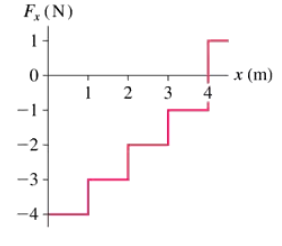
A 2.0 kg particle moving along the x-axis experiences the force shown in FIGURE EX9.22. The particle's velocity is 3.0 m/s at x = 0 m. At what point on the x-axis does the particle have a turning point?

A particle moving on the x-axis experiences a force given by F_x = qx², where q is a constant. How much work is done on the particle as it moves from x = 0 to x = d?

A 35-cm-long vertical spring has one end fixed on the floor. Placing a 2.2 kg physics textbook on the spring compresses it to a length of 29 cm. What is the spring constant?

A horizontal spring with spring constant 750 N/m is attached to a wall. An athlete presses against the free end of the spring, compressing it 5.0 cm. How hard is the athlete pushing?

A 10-cm-long spring is attached to the ceiling. When a 2.0 kg mass is hung from it, the spring stretches to a length of 15 cm. How long is the spring when a 3.0 kg mass is suspended from it?

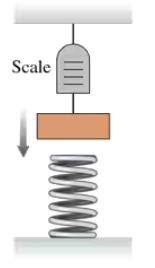
A 5.0 kg mass hanging from a spring scale is slowly lowered onto a vertical spring, as shown in FIGURE EX9.28. The scale reads in newtons. The scale reads 20 N when the lower spring has been compressed by 2.0 cm. What is the value of the spring constant for the lower spring?

A horizontal spring with spring constant 85 N/m extends outward from a wall just above floor level. A 1.5 kg box sliding across a frictionless floor hits the end of the spring and compresses it 6.5 cm before the spring expands and shoots the box back out. How fast was the box going when it hit the spring?

A 55 kg softball player slides into second base, generating 950 J of thermal energy in her legs and the ground. How fast was she running?

A baggage handler throws a 15 kg suitcase along the floor of an airplane luggage compartment with a speed of 1.2 m/s. The suitcase slides 2.0 m before stopping. Use work and energy to find the suitcase's coefficient of kinetic friction on the floor.

Justin, with a mass of 30 kg, is going down an 8.0-m-high water slide. He starts at rest, and his speed at the bottom is 11 m/s. How much thermal energy is created by friction during his descent?

An 8.0 kg crate is pulled 5.0 m up a 30° incline by a rope angled 18 ° above the incline. The tension in the rope is 120 N, and the crate's coefficient of kinetic friction on the incline is 0.25. What is the increase in thermal energy of the crate and incline?

How much work must you do to push a 10 kg block of steel across a steel table at a steady speed of 1.0m/s for 3.0 s? What is your power output while doing so?

How much work does an elevator motor do to lift a 1000 kg elevator a height of 100 m?

How much work does an elevator motor do to lift a 1000 kg elevator a height of 100 m? How much power must the motor supply to do this in 50 s at constant speed?

A 70 kg human sprinter can accelerate from rest to 10 m/s in 3.0 s. During the same time interval, a 30 kg greyhound can go from rest to 20 m/s. What is the average power output of each? Average power over a time interval ∆t is ∆E/∆t.

The energy used to pump liquids and gases through pipes is a significant fraction of the total energy consumption in the United States. Consider a small volume V of a liquid that has density ρ. Assume that the fluid is nonviscous so that friction with the pipe walls can be neglected. An upward-pushing force from a pump lifts this volume of fluid a height h at constant speed. How much work does the pump do?

A 1000 kg elevator accelerates upward at 1.0 m/s² for 10 m, starting from rest. How much work does the tension in the elevator cable do on the elevator?