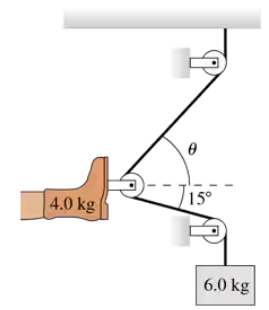
An accident victim with a broken leg is being placed in traction. The patient wears a special boot with a pulley attached to the sole. The foot and boot together have a mass of 4.0 kg, and the doctor has decided to hang a 6.0 kg mass from the rope. The boot is held suspended by the ropes, as shown in FIGURE P6.40, and does not touch the bed. Determine the amount of tension in the rope by using Newton's laws to analyze the hanging mass. Hint: If the pulleys are frictionless, which we will assume, the tension in the rope is constant from one end to the other.

Seat belts and air bags save lives by reducing the forces exerted on the driver and passengers in an automobile collision. Cars are designed with a 'crumple zone' in the front of the car. In the event of an impact, the passenger compartment decelerates over a distance of about 1 m as the front of the car crumples. An occupant restrained by seat belts and air bags decelerates with the car. By contrast, an unrestrained occupant keeps moving forward with no loss of speed (Newton's first law!) until hitting the dashboard or windshield. These are unyielding surfaces, and the unfortunate occupant then decelerates over a distance of only about 5 mm. A 60 kg person is in a head-on collision. The car's speed at impact is 15 m/s. Estimate the net force on the person if he or she is wearing a seat belt and if the air bag deploys.

Compressed air is used to fire a 50 g ball vertically upward from a 1.0-m-tall tube. The air exerts an upward force of 2.0 N on the ball as long as it is in the tube. How high does the ball go above the top of the tube? Neglect air resistance.

A rifle with a barrel length of 60 cm fires a 10 g bullet with a horizontal speed of 400 m/s. The bullet strikes a block of wood and penetrates to a depth of 12 cm. How long does it take the bullet to come to rest?

A rocket of mass m is launched straight up with thrust F_thrust. Find an expression for the rocket's speed at height h if air resistance is neglected.

The motor of a 350 g model rocket generates 9.5 N thrust. If air resistance can be neglected, what will be the rocket's speed as it reaches a height of 85 m?

Sam, whose mass is 75 kg, takes off across level snow on his jet-powered skis. The skis have a thrust of 200 N and a coefficient of kinetic friction on snow of 0.10. Unfortunately, the skis run out of fuel after only 10 s. What is Sam's top speed?

Sam, whose mass is 75 kg, takes off across level snow on his jet-powered skis. The skis have a thrust of 200 N and a coefficient of kinetic friction on snow of 0.10. Unfortunately, the skis run out of fuel after only 10 s. How far has Sam traveled when he finally coasts to a stop?

A baggage handler drops your 10 kg suitcase onto a conveyor belt running at 2.0 m/s. The materials are such that μ_s = 0.50 and μ_k = 0.30. How far is your suitcase dragged before it is riding smoothly on the belt?

A 5.0 kg wooden sled is launched up a 25° snow-covered slope with an initial speed of 10 m/s. What vertical height does the sled reach above its starting point?

A large box of mass M is moving on a horizontal surface at speed v₀. A small box of mass m sits on top of the large box. The coefficients of static and kinetic friction between the two boxes are μ_s and μ_k, respectively. Find an expression for the shortest distance d_min in which the large box can stop without the small box slipping.

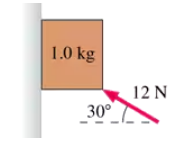
A 1.0 kg wood block is pressed against a vertical wood wall by the 12 N force shown in FIGURE P6.57. If the block is initially at rest, will it move upward, move downward, or stay at rest?

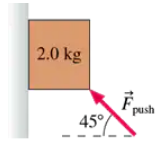
The 2.0 kg wood box in FIGURE P6.58 slides down a vertical wood wall while you push on it at a 45° angle. What magnitude of force should you apply to cause the box to slide down at a constant speed?

Astronauts in space 'weigh' themselves by oscillating on a spring. Suppose the position of an oscillating 75 kg astronaut is given by $x=\left(0.30\text{m}\right)\sin \left(\right(\pi \text{rad/s})\times t)$, where t is in s. What force does the spring exert on the astronaut at (a) t = 1.0 s and (b) 1.5 s? Note that the angle of the sine function is in radians.

A particle of mass m moving along the x-axis experiences the net force Fₓ = ct, where c is a constant. The particle has velocity v₀ₓ at t = 0. Find an algebraic expression for the particle's velocity vₓ at a later time t.

A 500 g ball moves horizontally with velocity v_𝓍 = ( 15 m) / (t + 1 s) for t > 0 s. What is the net force on the ball at t = 1 s?

A ball is shot from a compressed-air gun at twice its terminal speed. What is the ball's initial acceleration, as a multiple of g, if it is shot straight up?

What is the magnitude of the acceleration of a skydiver at the instant she is falling at one-half her terminal speed?

A block of mass m is at rest at the origin at t = 0. It is pushed with constant force F₀ from 𝓍 = 0 to 𝓍 = L across a horizontal surface whose coefficient of kinetic friction is μₖ = μ₀ ( 1 - 𝓍/L ) . That is, the coefficient of friction decreases from μ₀ at 𝓍 = 0 to zero at 𝓍 = L. b. Find an expression for the block's speed as it reaches position L.

A spherical particle of mass m is shot horizontally with initial speed v₀ into a viscous fluid. Use Stokes' law to find an expression for vₓ (t), the horizontal velocity as a function of time. Vertical motion due to gravity can be ignored.

A 4.0-cm-diameter, 55 g ball is shot horizontally into a tank of 40°C honey. How long will it take for the horizontal speed to decrease to 10% of its initial value?

A 1.0-cm-diameter, 2.0 g marble is shot horizontally into a tank of 20°C olive oil at 10 cm/s. How far in cm will it travel before stopping?

An object with cross section A is shot horizontally across frictionless ice. Its initial velocity is v₀ₓ at t₀ = 0 s. Air resistance is not negligible. Show that the velocity at time t is given by the expression $v_x=\frac{v_{0x}}{1+C_d\rho A{v}_{0x}t/2m}$.