A projectile's horizontal range over level ground is $\frac{v_0^2\sin 2\theta }{g}$. At what launch angle or angles will the projectile land at half of its maximum possible range?

A projectile is launched from ground level at angle θ and speed v₀ into a headwind that causes a constant horizontal acceleration of magnitude a opposite the direction of motion. Find an expression in terms of a and g for the launch angle that gives maximum range.

A projectile is launched from ground level at angle θ and speed v₀ into a headwind that causes a constant horizontal acceleration of magnitude a opposite the direction of motion. What is the angle for maximum range if a is 10% of g?

A gray kangaroo can bound across level ground with each jump carrying it 10 m from the takeoff point. Typically the kangaroo leaves the ground at a 20° angle. If this is so: What is its maximum height above the ground?

A ball is thrown toward a cliff of height h with a speed of 30 m/s and an angle of 60° above horizontal. It lands on the edge of the cliff 4.0 s later. What was the maximum height of the ball?

A ball is thrown toward a cliff of height h with a speed of 30 m/s and an angle of 60° above horizontal. It lands on the edge of the cliff 4.0 s later. What is the ball's impact speed?

You are watching an archery tournament when you start wondering how fast an arrow is shot from the bow. Remembering your physics, you ask one of the archers to shoot an arrow parallel to the ground. You find the arrow stuck in the ground 60 m away, making a 30° angle with the ground. How fast was the arrow shot?

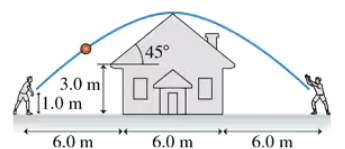
You're 6.0 m from one wall of the house seen in FIGURE P4.55. You want to toss a ball to your friend who is 6.0 m from the opposite wall. The throw and catch each occur 1.0 m above the ground. At what angle should you toss the ball?

A cannonball is fired at 100 m/s from a barrel tilted upward at 25°. What is the angle after the cannonball travels 500 m?

Ships A and B leave port together. For the next two hours, ship A travels at 20 mph in a direction 30° west of north while ship B travels 20° east of north at 25 mph. What is the speed of ship A as seen by ship B?

While driving north at 25 m/s during a rainstorm you notice that the rain makes an angle of 38° with the vertical. While driving back home moments later at the same speed but in the opposite direction, you see that the rain is falling straight down. From these observations, determine the speed and angle of the raindrops relative to the ground.

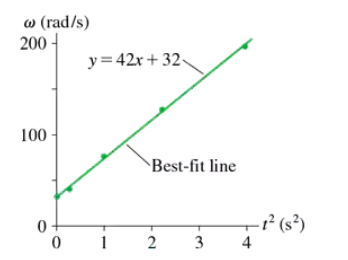
The angular velocity of a spinning gyroscope is measured every 0.5 s. The results and the best-fit line from a spreadsheet are shown in FIGURE P4.63. What is the gyroscope's initial angular velocity at t = 0 s?

A ball rolling on a circular track, starting from rest, has angular acceleration $\alpha$. Find an expression, in terms of $\alpha$, for the time at which the ball's acceleration vector a is ${45}^{\circ }$ away from a radial line toward the center of the circle.

A typical laboratory centrifuge rotates at 4000 rpm. Test tubes have to be placed into a centrifuge very carefully because of the very large accelerations. What is the acceleration at the end of a test tube that is 10 cm from the axis of rotation?

A typical laboratory centrifuge rotates at 4000 rpm. Test tubes have to be placed into a centrifuge very carefully because of the very large accelerations. For comparison, what is the magnitude of the acceleration a test tube would experience if dropped from a height of 1.0 m and stopped in a 1.0-ms-long encounter with a hard floor?

A Ferris wheel of radius R speeds up with angular acceleration starting from rest. Find expressions for the (a) velocity and (b) centripetal acceleration of a rider after the Ferris wheel has rotated through angle ∆θ.

Communications satellites are placed in a circular orbit where they stay directly over a fixed point on the equator as the earth rotates. These are called geosynchronous orbits. The radius of the earth is 6.37 x 10⁶ m, and the altitude of a geosynchronous orbit is 3.58 x 10⁷ m (≈ 22,000 miles). What are (a) the speed and (b) the magnitude of the acceleration of a satellite in a geosynchronous orbit?

A computer hard disk 8.0 cm in diameter is initially at rest. A small dot is painted on the edge of the disk. The disk accelerates at 600 rad/s² for ½ s, then coasts at a steady angular velocity for another ½ s. Through how many revolutions has the disk turned?

Flywheels—rapidly rotating disks—are widely used in industry for storing energy. They are spun up slowly when extra energy is available, then decelerate quickly when needed to supply a boost of energy. A 20-cm-diameter rotor made of advanced materials can spin at 100,000 rpm. What is the speed of a point on the rim of this rotor?

Flywheels—rapidly rotating disks—are widely used in industry for storing energy. They are spun up slowly when extra energy is available, then decelerate quickly when needed to supply a boost of energy. A 20-cm-diameter rotor made of advanced materials can spin at 100,000 rpm. b. Suppose the rotor's angular velocity decreases by 40% over 30 s as it supplies energy. What is the magnitude of the rotor's angular acceleration? Assume that the angular acceleration is constant.

A 25 g steel ball is attached to the top of a 24-cm-diameter vertical wheel. Starting from rest, the wheel accelerates at 470 rad/s². The ball is released after ¾ of a revolution. How high does it go above the center of the wheel?

The angular velocity of a process control motor is ω = ( 20 - ½ t² ) rad/s, where t is in seconds. At what time does the motor reverse direction?

The angular velocity of a process control motor is ω = ( 20 ─ ½ t² ) rad/s, where t is in seconds. Through what angle does the motor turn between t = 0 s and the instant at which it reverses direction?

A 6.0-cm-diameter gear rotates with angular velocity ω = ( 20 ─ ½ t² ) rad/s where t is in seconds. At t = 4.0 s, what are: The gear's angular acceleration?

A 6.0-cm-diameter gear rotates with angular velocity ω = ( 20 ─ ½ t² ) rad/s where t is in seconds. At t = 4.0 s, what are: The tangential acceleration of a tooth on the gear?

A painted tooth on a spinning gear has angular position θ = (6.0 rad/s⁴)t⁴. What is the tooth's angular acceleration at the end of 10 revolutions?

In Problems 78, 79, and 80 you are given the equations that are used to solve a problem. For each of these, you are to write a realistic problem for which these are the correct equations. Be sure that the answer your problem requests is consistent with the equations given.

$\begin{aligned} 100 \, \text{m} &= 0 \, \text{m} + (50 \cos \theta \, \text{m/s}) t_1 \\ 0 \, \text{m} &= 0 \, \text{m} + (50 \sin \theta \, \text{m/s}) t_1 - \frac{1}{2} (9.80 \, \text{m/s}^2) t_1^2 \end{aligned}$

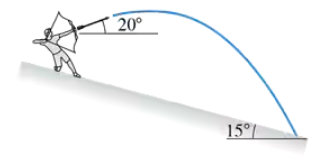
An archer standing on a 15° slope shoots an arrow 20° above the horizontal, as shown in FIGURE CP4.82. How far down the slope does the arrow hit if it is shot with a speed of 5.0 m/s from 1.75 m above the ground?

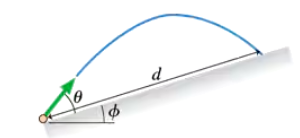
The cannon in FIGURE CP4.83 fires a projectile at launch angle θ with respect to the slope, which is at angle Φ. Find the launch angle that maximizes d. Hint: Choosing the proper coordinate system is essential. There are two options.

A cannon on a flat railroad car travels to the east with its barrel tilted 30° above horizontal. It fires a cannonball at 50 m/s. At t = 0 s , the car, starting from rest, begins to accelerate to the east at 2.0 m/s². At what time should the cannon be fired to hit a target on the tracks that is 400 m to the east of the car's initial position? Assume that the cannonball is fired from ground level.