Back
BackProblem 2a
Complete the motion diagram by adding acceleration vectors.
Problem 4a
At this instant, the particle is speeding up and curving upward. What is the direction of its acceleration?
Problem 5b
Is this particle curving upward, curving downward, or moving in a straight line?
Problem 6a
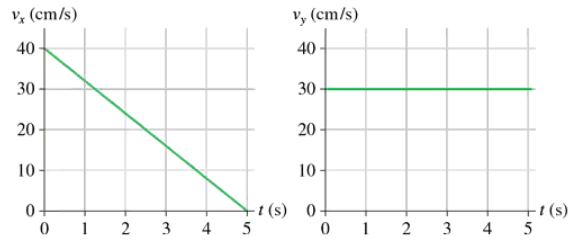
A rocket-powered hockey puck moves on a horizontal frictionless table. FIGURE EX4.6 shows graphs of vx and vy, the x- and y-components of the puck's velocity. The puck starts at the origin. In which direction is the puck moving at t = 2s? Give your answer as an angle from the x-axis.
Problem 6b
A rocket-powered hockey puck moves on a horizontal frictionless table. FIGURE EX4.6 shows graphs of vx and vy, the x- and y-components of the puck's velocity. The puck starts at the origin. How far from the origin is the puck at t = 5s?
Problem 7
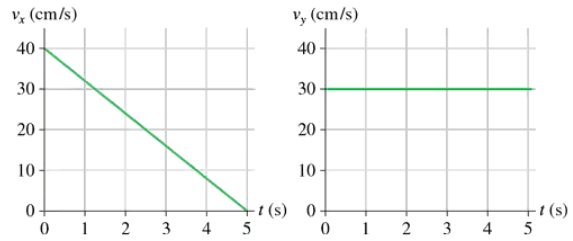
A rocket-powered hockey puck moves on a horizontal frictionless table. Figure EX4.7 shows graphs of vx and vy the x- and y-components of the puck's velocity. The puck starts at the origin. What is the magnitude of the puck's acceleration at t = 5s?
Problem 8a
A particle moving in the xy-plane has velocity v = (2ti + (3-t2)j) m/s, where t is in s. What is the particle's acceleration vector at t = 4s?
Problem 9a
A particle's trajectory is described by where is in . What are the particle's position and speed at and ?
Problem 9b
A particle's trajectory is described by where is in . What is the particle's direction of motion, measured as an angle from the -axis, at and ?
Problem 10a
You have a remote-controlled car that has been programmed to have velocity , where t is in s. At t = 0 s, the car is at . What are the car's position vector?
Problem 12
A supply plane needs to drop a package of food to scientists working on a glacier in Greenland. The plane flies 100 m above the glacier at a speed of 150 m/s. How far short of the target should it drop the package?
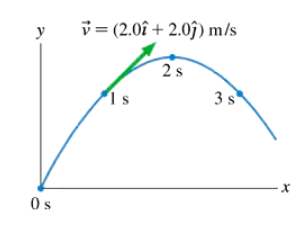
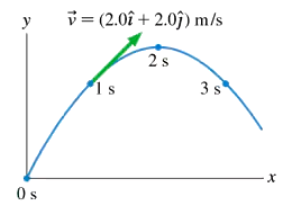
Problem 13a
A physics student on Planet Exidor throws a ball, and it follows the parabolic trajectory shown in FIGURE EX4.13. The ball's position is shown at 1 s intervals until t = 3s. At t = 1s, the ball's velocity is v = (2.0 i + 2.0 j) m/s. Determine the ball's velocity at t = 0 s, 2s, and 3s.
Problem 13b
A physics student on Planet Exidor throws a ball, and it follows the parabolic trajectory shown in FIGURE EX4.13. The ball's position is shown at 1 s intervals until t = 3s. At t = 1s, the ball's velocity is v = (2.0 i + 2.0 j) m/s. What is the value of g on Planet Exidor?
Problem 15b
A rifle is aimed horizontally at a target 50 m away. The bullet hits the target 2.0 cm below the aim point. (b) What was the bullet's speed as it left the barrel?
Problem 17b
On the Apollo 14 mission to the moon, astronaut Alan Shepard hit a golf ball with a 6 iron. The free-fall acceleration on the moon is 1/6 of its value on earth. Suppose he hit the ball with a speed of 25 m/s at an angle 30 degrees above the horizontal. For how much more time was the ball in flight?
Problem 21b
A kayaker needs to paddle north across a 100-m-wide harbor. The tide is going out, creating a tidal current that flows to the east at 2.0 m/s. The kayaker can paddle with a speed of 3.0 m/s. How long will it take him to cross?
Problem 22
Susan, driving north at 60 mph, and Trent, driving east at 45 mph, are approaching an intersection. What is Trent's speed relative to Susan's reference frame?
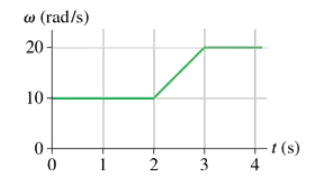
Problem 23
FIGURE EX4.23 shows the angular-velocity-versus-time graph for a particle moving in a circle. How many revolutions does the object make during the first 4 s?
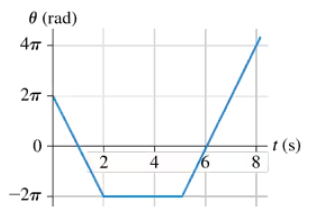
Problem 24b
FIGURE EX4.24 shows the angular-position-versus-time graph for a particle moving in a circle. What is the particle's angular velocity at t = 4s
Problem 27
The earth's radius is about 4000 miles. Kampala, the capital of Uganda, and Singapore are both nearly on the equator. The distance between them is 5000 miles. The flight from Kampala to Singapore takes 9.0 hours. What is the plane's angular velocity with respect to the earth's surface? Give your answer in °/h.
Problem 28a
As the earth rotates, what is the speed of a physics student in Miami, Florida, at latitude 26°. Ignore the revolution of the earth around the sun. The radius of the earth is 6400 km.
Problem 31
Peregrine falcons are known for their maneuvering ability. In a tight circular turn, a falcon can attain a centripetal acceleration 1.5 times the free-fall acceleration. What is the radius of the turn if the falcon is flying at 25 m/s?
Problem 33a
The radius of the earth's very nearly circular orbit around the sun is 1.5 x 1011 m. Find the magnitude of the earth's velocity.
Problem 33b
The radius of the earth's very nearly circular orbit around the sun is 1.5 x 1011 m. Find the magnitude of the earth's angular velocity.
Problem 34b
A speck of dust on a spinning DVD has a centripetal acceleration of 20 m/s3 . What would be the acceleration of the first speck of dust if the disk's angular velocity was doubled?
Problem 35
Your roommate is working on his bicycle and has the bike upside down. He spins the 60-cm-diameter wheel, and you notice that a pebble stuck in the tread goes by three times every second. What are the pebble's speed and acceleration?
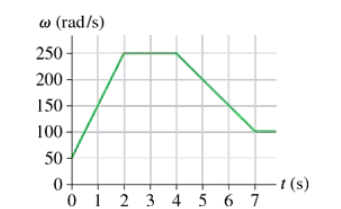
Problem 36b
FIGURE EX4.36 shows the angular velocity graph of the crankshaft in a car. What is the crankshaft's angular acceleration at t = 3s
Problem 40b
A 5.0-m-diameter merry-go-round is initially turning with a 4.0 s period. It slows down and stops in 20 s. How many revolutions does the merry-go-round make as it stops?
Problem 43
Starting from rest, a DVD steadily accelerates to 500 rpm in 1.0 s, rotates at this angular speed for 3.0 s, then steadily decelerates to a halt in 2.0 s. How many revolutions does it make?
Problem 44
A spaceship maneuvering near Planet Zeta is located at relative to the planet, and traveling at . It turns on its thruster engine and accelerates with for . What is the spaceship's position when the engine shuts off? Give your answer as a position vector measured in .