The position of a particle as a function of time is given by $\overrightarrow{r}$ = ( 5.0î ＋4.0ĵ )t² m where t is in seconds. Find an expression for the particle's velocity $\overrightarrow{v}$ as a function of time.

The position of a particle as a function of time is given by $\overrightarrow{r}$ = ( 5.0î ＋4.0ĵ )t² m where t is in seconds. What is the particle's speed at t = 0, 2, and 5 s?

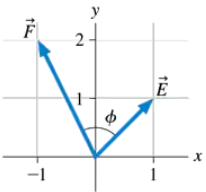
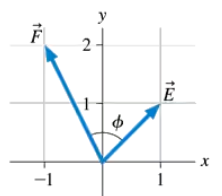
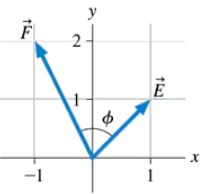
What is the angle Φ between vectors E and F in FIGURE P3.24?

Use geometry and trigonometry to determine the magnitude and direction of G = E＋F.

Use components to determine the magnitude and direction of G = E＋F.

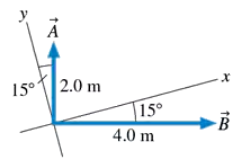
FIGURE P3.26 shows vectors A and B. Find D = 2A ＋B Write your answer in component form.

Find a vector that points in the same direction as the vector ( î ＋ ĵ ) and whose magnitude is 1.

The minute hand on a watch is 2.0 cm in length. What is the displacement vector of the tip of the minute hand in each case? Use a coordinate system in which the y-axis points toward the 12 on the watch face. From 8:00 to 8:20 a.m.

The minute hand on a watch is 2.0 cm in length. What is the displacement vector of the tip of the minute hand in each case? Use a coordinate system in which the y-axis points toward the 12 on the watch face. From 8:00 to 9:00 a.m.

While vacationing in the mountains you do some hiking. In the morning, your displacement is $S_{morning}=(2000\text{m},\text{east})+(3000\text{m},\text{north})+(200\text{m},\text{vertical})$. Continuing on after lunch, your displacement is $S_{afternoon}=(1500\text{m},\text{west})+(2000\text{m},\text{north})-(300\text{m},\text{vertical})$. At the end of the hike, how much higher or lower are you compared to your starting point?

While vacationing in the mountains you do some hiking. In the morning, your displacement is $\mathbf{S}_{morning} = (2000 \, \text{m}, \text{east}) + (3000 \, \text{m}, \text{north}) + (200 \, \text{m}, \text{vertical})$. Continuing on after lunch, your displacement is $\mathbf{S}_{afternoon} = (1500 \, \text{m}, \text{west}) + (2000 \, \text{m}, \text{north}) - (300 \, \text{m}, \text{vertical})$. What is the magnitude of your net displacement for the day?

Trevon drives with velocity v₁ = (55î - 10ĵ) mph for 1.0 h, then v₂ = (20î ＋ 50ĵ) mph for 2.0 h. What is Trevon's displacement? Write your answer in component form using unit vectors.

Ruth sets out to visit her friend Ward, who lives 50 mi north and 100 mi east of her. She starts by driving east, but after 30 mi she comes to a detour that takes her 15 mi south before going east again. She then drives east for 8 mi and runs out of gas, so Ward flies there in his small plane to get her. What is Ward's displacement vector? Give your answer (a) in component form, using a coordinate system in which the y-axis points north, and (b) as a magnitude and direction.

A cannon tilted upward at 30° fires a cannonball with a speed of 100 m/s. What is the component of the cannonball's velocity parallel to the ground?

A cannonball leaves the barrel with velocity v = (75î ＋ 45ĵ). At what angle is the barrel tilted above horizontal?

You are fixing the roof of your house when a hammer breaks loose and slides down. The roof makes an angle of 35° with the horizontal, and the hammer is moving at 4.5 m/s when it reaches the edge. What are the horizontal and vertical components of the hammer's velocity just as it leaves the roof?

Jack and Jill ran up the hill at 3.0 m/s. The horizontal component of Jill's velocity vector was 2.5 m/s. What was the angle of the hill?

Jack and Jill ran up the hill at 3.0 m/s. The horizontal component of Jill's velocity vector was 2.5 m/s. What was the vertical component of Jill's velocity?

Kami is walking through the airport with her two-wheeled suitcase. The suitcase handle is tilted 40° from vertical, and Kami pulls parallel to the handle with a force of 120 N. (Force is measured in newtons, abbreviated N.) What are the horizontal and vertical components of her applied force?

A jet plane taking off from an aircraft carrier has acceleration a = ( 15 m/s², 22° above horizontal). What are the horizontal and vertical components of the jet's acceleration?

Your neighbor Paul has rented a truck with a loading ramp. The ramp is tilted upward at 25°, and Paul is pulling a large crate up the ramp with a rope that angles 10° above the ramp. If Paul pulls with a force of 550 N, what are the horizontal and vertical components of his force? (Force is measured in newtons, abbreviated N.)

Tom is climbing a 3.0-m-long ladder that leans against a vertical wall, contacting the wall 2.5 m above the ground. His weight of 680 N is a vector pointing vertically downward. (Weight is measured in newtons, abbreviated N.) What are the components of Tom's weight parallel and perpendicular to the ladder?

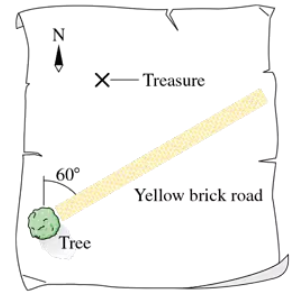
The treasure map in FIGURE P3.41 gives the following directions to the buried treasure: 'Start at the old oak tree, walk due north for 500 paces, then due east for 100 paces. Dig.' But when you arrive, you find an angry dragon just north of the tree. To avoid the dragon, you set off along the yellow brick road at an angle 60° east of north. After walking 300 paces you see an opening through the woods. In which direction should you walk, as an angle west of north, and how far, to reach the treasure?

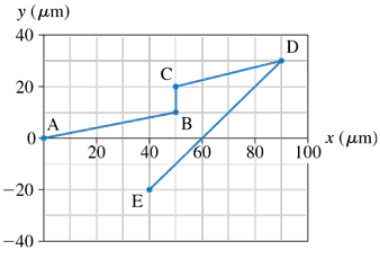
The bacterium E. coli is a single-cell organism that lives in the gut of healthy animals, including humans. When grown in a uniform medium in the laboratory, these bacteria swim along zig-zag paths at a constant speed of 20 μm/s. FIGURE P3.42 shows the trajectory of an E. coli as it moves from point A to point E. What are the magnitude and direction of the bacterium's average velocity for the entire trip?

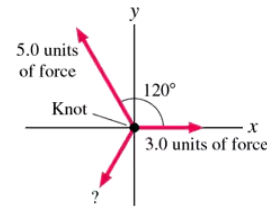
FIGURE P3.43 shows three ropes tied together in a knot. One of your friends pulls on a rope with 3.0 units of force and another pulls on a second rope with 5.0 units of force. How hard and in what direction must you pull on the third rope to keep the knot from moving? Give the direction as an angle below the negative x-axis.

A crate, seen from above, is pulled with three ropes that have the tensions shown in FIGURE P3.44. Tension is a vector directed along the rope, measured in newtons (abbreviated N). Suppose the three ropes are replaced with a single rope that has exactly the same effect on the crate. What is the tension in this rope? Write your answer in component form using unit vectors.

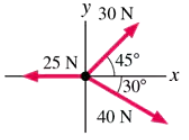
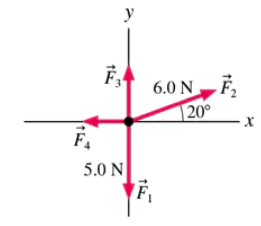
Four forces are exerted on the object shown in FIGURE $P3.45$. (Forces are measured in newtons, abbreviated $\text{N}$.) The net force on the object is ${\vec{F}}_{\text{net}}={\vec{F}}_1+{\vec{F}}_2+{\vec{F}}_3+{\vec{F}}_4=4.0\hat{i}\text{N}$. What are (a) ${\vec{F}}_3$ and (b) ${\vec{F}}_4$? Give your answers in component form.

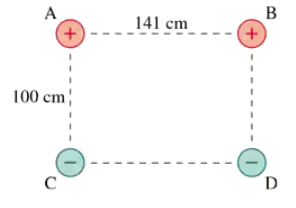
FIGURE P3.46 shows four electric charges located at the corners of a rectangle. Like charges, you will recall, repel each other while opposite charges attract. Charge B exerts a repulsive force (directly away from B) on charge A of 3.0 N. Charge C exerts an attractive force (directly toward C) on charge A of 6.0 N. Finally, charge D exerts an attractive force of 2.0 N on charge A. Assuming that forces are vectors, what are the magnitude and direction of the net force F_net exerted on charge A?