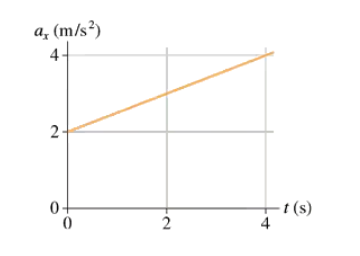Back
BackProblem 14
A jet plane is cruising at 300 m/s when suddenly the pilot turns the engines up to full throttle. After traveling 4.0 km, the jet is moving with a speed of 400 m/s. What is the magnitude of the jet's acceleration, assuming it to be a constant acceleration?
Problem 16
When you sneeze, the air in your lungs accelerates from rest to 150 km/h in approximately 0.50 s. What is the magnitude of the acceleration of the air in m/s2?
Problem 17
A speed skater moving to the left across frictionless ice at 8.0 m/s hits a 5.0-m-wide patch of rough ice. She slows steadily, then continues on at 6.0 m/s. What is her acceleration on the rough ice?
Problem 18
A Porsche challenges a Honda to a 400 m race. Because the Porsche's acceleration of 3.5 m/s2 is larger than the Honda's 3.0 m/s2, the Honda gets a 1.0 s head start. Who wins? By how many seconds?
Problem 18b
FIGURE EX1.18 shows the motion diagram of a drag racer. The camera took one frame every 2 s. Make a position-versus-time graph for the drag racer. Because you have data only at certain instants, your graph should consist of dots that are not connected together.
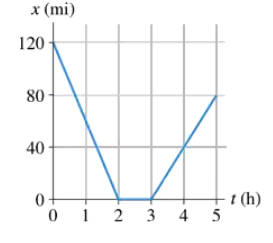
Problem 20
Write a short description of the motion of a real object for which FIGURE EX1.20 would be a realistic position-versus-time graph.
Problem 20a
Ball bearings are made by letting spherical drops of molten metal fall inside a tall tower—called a shot tower—and solidify as they fall. If a bearing needs 4.0 s to solidify enough for impact, how high must the tower be?
Problem 20b
Ball bearings are made by letting spherical drops of molten metal fall inside a tall tower—called a shot tower—and solidify as they fall. What is the bearing's impact velocity?
Problem 21a
A rock is tossed straight up from ground level with a speed of 20 m/s. When it returns, it falls into a hole 10 m deep. What is the rock's speed as it hits the bottom of the hole?
Problem 23
As a science project, you drop a watermelon off the top of the Empire State Building, 320 m above the sidewalk. It so happens that Superman flies by at the instant you release the watermelon. Superman is headed straight down with a speed of 35 m/s. How fast is the watermelon going when it passes Superman?
Problem 24
When jumping, a flea accelerates at an astounding 1000 m/s2, but over only the very short distance of 0.50 mm. If a flea jumps straight up, and if air resistance is neglected (a rather poor approximation in this situation), how high does the flea go?
Problem 26
A car traveling at 30 m/s runs out of gas while traveling up a 10° slope. How far up the hill will it coast before starting to roll back down?
Problem 27a
A skier is gliding along at 3.0 m/s on horizontal, frictionless snow. He suddenly starts down a 10° incline. His speed at the bottom is 15 m/s. What is the length of the incline?
Problem 29
A bicycle coasting at 8.0 m/s comes to a 5.0-m-long, 1.0-m-high ramp. What is the bicycle's speed as it leaves the top of the ramp?
Problem 30b
A snowboarder glides down a 50-m-long, 15° hill. She then glides horizontally for 10 m before reaching a 25° upward slope. Assume the snow is frictionless. How far can she travel up the 25° slope?
Problem 31
FIGURE EX2.31 shows the acceleration-versus-time graph of a particle moving along the x-axis. Its initial velocity is v0x = 8.0 m/s at t0 = 0 s. What is the particle’s velocity at t = 4.0s?
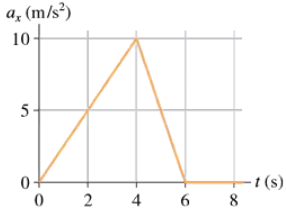
Problem 32
FIGURE EX2.32 shows the acceleration graph for a particle that starts from rest at t = 0 s. What is the particle's velocity at t = 6 s?
Problem 33a
A particle moving along the x-axis has its position described by the function x = (2t3 + 2t + 1) m, where t is in s. At t = 2s, what are the particle's position?
Problem 34a
A particle moving along the x-axis has its veocity described by the function vx = 2t2 m/s, where t is in s. itsinitial position is x0 = 1 m at t0 = 0 s. At t = 1 s, what are the particle's position?
Problem 35b
The vertical position of a particle is given by the function y = (t2 - 4t + 2) m, where t is in s. What is the particle's position at that time?
Problem 36a
The position of a particle is given by the function x = (2t3 = 6t2 + 12) m, where t is in s. At what time does the particle reach its minimum velocity? What is (vx)min?
Problem 36b
The position of a particle is given by the function x = (2t3 - 6t2 + 12) m, where t is in s. At what time is the acceleration zero?
Problem 38a
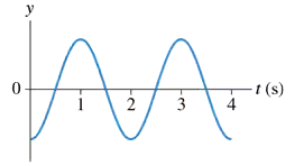
A block is suspended from a spring, pulled down, and released. The block's position-versus-time graph is shown in FIGURE P2.38. At what times is the velocity zero? At what times is the velocity most positive? Most negative?
Problem 38b
A block is suspended from a spring, pulled down, and released. The block's position-versus-time graph is shown in FIGURE P2.38. Draw a reasonable velocity-versus-time graph.
Problem 39b
A particle's velocity is described by the function vₓ = (t² - 7t + 10) m/s, where t is in s. What is the particle's acceleration at each of the turning points?
Problem 40
A particle's velocity is described by the function vₓ =kt² m/s, where k is a constant and t is in s. The particle's position at t₀ = 0 s is x₀ = -9.0 m. At t₁ = 3.0 s, the particle is at x₁ = 9.0 m. Determine the value of the constant k. Be sure to include the proper units.
Problem 42a
A particle's velocity is given by the function , where is in . What is the first time after when the particle reaches a turning point?
Problem 42b
A particle's velocity is given by the function , where is in . What is the particle's acceleration at that time?
Problem 44
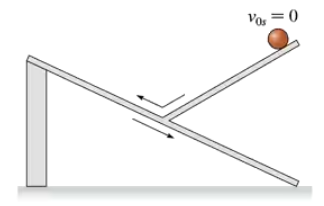
Draw position, velocity, and acceleration graphs for the ball shown in FIGURE P2.44. See Problem 43 for more information.
Problem 45
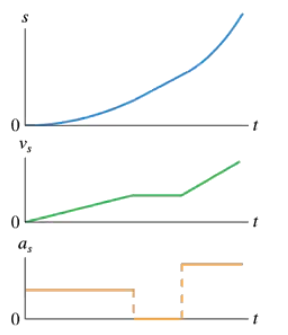
FIGURE P2.45 shows a set of kinematic graphs for a ball rolling on a track. All segments of the track are straight lines, but some may be tilted. Draw a picture of the track and also indicate the ball's initial condition.