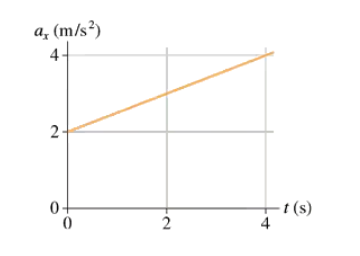Back
BackProblem 31
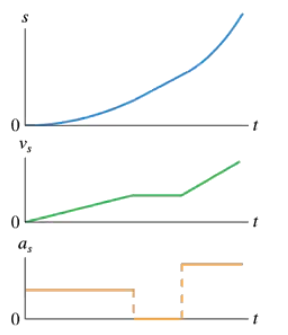
FIGURE EX2.31 shows the acceleration-versus-time graph of a particle moving along the x-axis. Its initial velocity is v0x = 8.0 m/s at t0 = 0 s. What is the particle’s velocity at t = 4.0s?
Problem 32
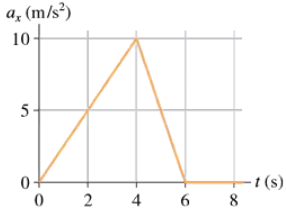
FIGURE EX2.32 shows the acceleration graph for a particle that starts from rest at t = 0 s. What is the particle's velocity at t = 6 s?
Problem 33a
A particle moving along the x-axis has its position described by the function x = (2t3 + 2t + 1) m, where t is in s. At t = 2s, what are the particle's position?
Problem 34a
A particle moving along the x-axis has its veocity described by the function vx = 2t2 m/s, where t is in s. itsinitial position is x0 = 1 m at t0 = 0 s. At t = 1 s, what are the particle's position?
Problem 35b
The vertical position of a particle is given by the function y = (t2 - 4t + 2) m, where t is in s. What is the particle's position at that time?
Problem 36a
The position of a particle is given by the function x = (2t3 = 6t2 + 12) m, where t is in s. At what time does the particle reach its minimum velocity? What is (vx)min?
Problem 36b
The position of a particle is given by the function x = (2t3 - 6t2 + 12) m, where t is in s. At what time is the acceleration zero?
Problem 38a
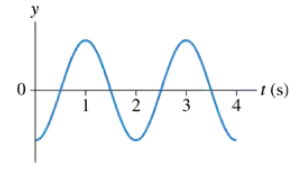
A block is suspended from a spring, pulled down, and released. The block's position-versus-time graph is shown in FIGURE P2.38. At what times is the velocity zero? At what times is the velocity most positive? Most negative?
Problem 38b
A block is suspended from a spring, pulled down, and released. The block's position-versus-time graph is shown in FIGURE P2.38. Draw a reasonable velocity-versus-time graph.
Problem 39b
A particle's velocity is described by the function vₓ = (t² - 7t + 10) m/s, where t is in s. What is the particle's acceleration at each of the turning points?
Problem 40
A particle's velocity is described by the function vₓ =kt² m/s, where k is a constant and t is in s. The particle's position at t₀ = 0 s is x₀ = -9.0 m. At t₁ = 3.0 s, the particle is at x₁ = 9.0 m. Determine the value of the constant k. Be sure to include the proper units.
Problem 42a
A particle's velocity is given by the function , where is in . What is the first time after when the particle reaches a turning point?
Problem 42b
A particle's velocity is given by the function , where is in . What is the particle's acceleration at that time?
Problem 44
Draw position, velocity, and acceleration graphs for the ball shown in FIGURE P2.44. See Problem 43 for more information.
Problem 45
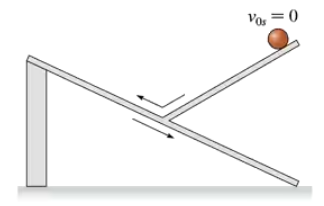
FIGURE P2.45 shows a set of kinematic graphs for a ball rolling on a track. All segments of the track are straight lines, but some may be tilted. Draw a picture of the track and also indicate the ball's initial condition.
Problem 47
You are driving to the grocery store at 20 m/s. You are 110 m from an intersection when the traffic light turns red. Assume that your reaction time is 0.50 s and that your car brakes with constant acceleration. What magnitude braking acceleration will bring you to a stop exactly at the intersection?
Problem 48a
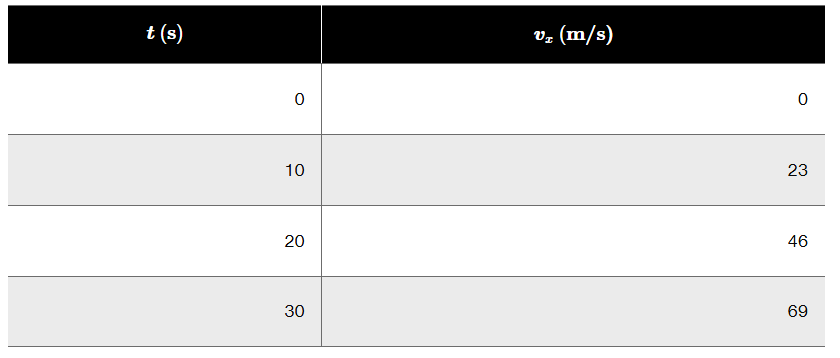
The takeoff speed for an Airbus A320 jetliner is 80 m/s. Velocity data measured during takeoff are as shown. Is the jetliner's acceleration constant during takeoff? Explain.
Problem 49a
You're driving down the highway late one night at 20 m/s when a deer steps onto the road 35 m in front of you. Your reaction time before stepping on the brakes is 0.50 s, and the maximum deceleration of your car is 10 m/s². How much distance is between you and the deer when you come to a stop?
Problem 51
A car starts from rest at a stop sign. It accelerates at 4.0 m/s² for 6.0 s, coasts for 2.0 s, and then slows down at a rate of 3.0 m/s² for the next stop sign. How far apart are the stop signs?
Problem 52
A cheetah spots a Thomson's gazelle, its preferred prey, and leaps into action, quickly accelerating to its top speed of 30 m/s, the highest of any land animal. However, a cheetah can maintain this extreme speed for only 15 s before having to let up. The cheetah is 170 m from the gazelle as it reaches top speed, and the gazelle sees the cheetah at just this instant. With negligible reaction time, the gazelle heads directly away from the cheetah, accelerating at 4.6 m/s² for 5.0 s, then running at constant speed. Does the gazelle escape? If so, by what distance is the gazelle in front when the cheetah gives up?
Problem 53a
Find an expression for the minimum stopping distance dstop of a car traveling at speed v0 if the driver's reaction time is Treact and the magnitude of the acceleration during maximum braking is a constant abrake.
Problem 55
A 1000 kg weather rocket is launched straight up. The rocket motor provides a constant acceleration for 16 s, then the motor stops. The rocket altitude 20 s after launch is 5100 m. You can ignore any effects of air resistance. What was the rocket's acceleration during the first 16 s?
Problem 56a
A 200 kg weather rocket is loaded with 100 kg of fuel and fired straight up. It accelerates upward at 30 m/s² for 30 s, then runs out of fuel. Ignore any air resistance effects. What is the rocket's maximum altitude?
Problem 57
A lead ball is dropped into a lake from a diving board 5.0 m above the water. After entering the water, it sinks to the bottom with a constant velocity equal to the velocity with which it hit the water. The ball reaches the bottom 3.0 s after it is released. How deep is the lake?
Problem 58b
A hotel elevator ascends 200 m with a maximum speed of 5.0 m/s. Its acceleration and deceleration both have a magnitude of 1.0 m/s2. How long does it take to make the complete trip from bottom to top?
Problem 60b
You are 9.0 m from the door of your bus, behind the bus, when it pulls away with an acceleration of 1.0 m/s². You instantly start running toward the still-open door at 4.5 m/s. What is the maximum time you can wait before starting to run and still catch the bus?
Problem 61c
Ann and Carol are driving their cars along the same straight road. Carol is located at x = 2.4 mi at t = 0 h and drives at a steady 36 mph. Ann, who is traveling in the same direction, is located at x = 0.0 mi at t = 0.50 h and drives at a steady 50 mph. Draw a position-versus-time graph showing the motion of both Ann and Carol.
Problem 62
A steel ball rolls across a 30-cm-wide felt pad, starting from one edge. The ball's speed has dropped to half after traveling 20 cm. Will the ball stop on the felt pad or roll off?
Problem 63
A very slippery block of ice slides down a smooth ramp tilted at angle θ. The ice is released from rest at vertical height h above the bottom of the ramp. Find an expression for the speed of the ice at the bottom.
Problem 64
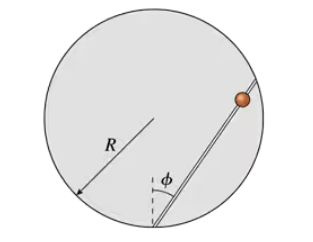
FIGURE P2.64 shows a fixed vertical disk of radius R. A thin, frictionless rod is attached to the bottom point of the disk and to a point on the edge, making angle Φ (Greek phi) with the vertical. Find an expression for the time it takes a bead to slide from the top end of the rod to the bottom.