Back
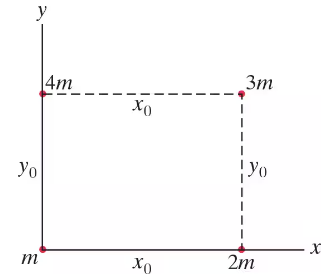
BackProblem 10
Four masses are arranged as shown in Fig. 6–28. Determine the x and y components of the gravitational force on the mass at the origin (m). Write the force in vector notation (î, ĵ).
Problem 25a
Use the binomial expansion to show that the value of g is altered by approximately at a height ∆r above the Earth’s surface, where rE is the radius of the Earth, as long as ∆r ≪ rE.
Problem 25b
The value of g is altered by approximately at a height ∆r above the Earth’s surface, where rE is the radius of the Earth, as long as ∆r ≪ rE. What is the meaning of the minus sign in this relation?
Problem 44b
An inclined plane, fixed to the inside of an elevator, makes a 38° angle with the floor. A mass m slides on the plane without friction. What is its acceleration relative to the plane if the elevator accelerates downward at 0.50 g?
Problem 44c
An inclined plane, fixed to the inside of an elevator, makes a 38° angle with the floor. A mass m slides on the plane without friction. What is its acceleration relative to the plane if the elevator falls freely?
Problem 44d
An inclined plane, fixed to the inside of an elevator, makes a 38° angle with the floor. A mass m slides on the plane without friction. What is its acceleration relative to the plane if the elevator moves upward at constant speed?
Problem 50
Determine the mean distance from Jupiter for each of Jupiter’s principal moons, using Kepler’s third law. Use the mean distance of Io and the periods given in Table 6–3. Compare your results to the values in Table 6–3.
Problem 72a
A satellite circles a spherical planet of unknown mass in a circular orbit of radius 1.6 x 10⁷ m. The magnitude of the gravitational force exerted on the satellite by the planet is 120 N. What would be the magnitude of the gravitational force exerted on the satellite by the planet if the radius of the orbit were increased to 3.0 x 10⁷m?
Problem 79
A particle is released at a height rE (radius of Earth) above the Earth’s surface. Determine its velocity when it hits the Earth. Ignore air resistance. [Hint: Use Newton’s second law, the law of universal gravitation, the chain rule, and integrate.]
Problem 80c
A plumb bob (a mass m hanging on a string) is deflected from the vertical by an angle θ due to a massive mountain nearby (Fig. 6–37). Estimate the angle θ of the plumb bob if it is 5 km from the center of Mt. Everest.