Suppose you are standing on a train accelerating at 0.20 g. What minimum coefficient of static friction must exist between your feet and the floor if you are not to slide?

(II) How large must the coefficient of static friction be between the tires and the road if a car is to round a level curve of radius 85 m at a speed of 95 km/h?

Show that if a skier moves at constant speed straight down a slope of angle θ (Example 5–6), then the coefficient of kinetic friction between skis and snow is μₖ = tanθ. Ignore air resistance.

Police investigators, examining the scene of an accident involving a car and an old truck, measure 72-m-long skid marks for the truck, which nearly came to a stop before colliding with the car at rest. The coefficient of kinetic friction between rubber and the pavement is about 0.80. Estimate the initial speed of the truck assuming a level road.

Piles of snow on slippery roofs can become dangerous projectiles as they melt. Consider a chunk of snow at the ridge of a roof with a slope of 24°. As the snow begins to melt, the coefficient of static friction decreases and the snow finally slips. Assuming that the distance from a chunk of snow to the edge of the roof is 6.0 m and the coefficient of kinetic friction is 0.20, calculate the speed of the snow chunk when it slides off the roof.

A flatbed truck is carrying a heavy crate. The coefficient of static friction between the crate and the bed of the truck is 0.75. What is the maximum rate at which the driver can decelerate and still avoid having the crate slide against the cab of the truck?

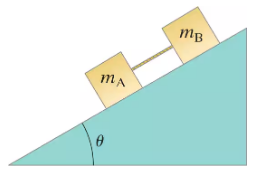
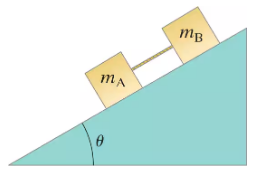
Two blocks made of different materials connected together by a thin cord slide down a ramp inclined at an angle θ to the horizontal, Fig. 5–40 (block B is above block A). The masses of the blocks are m_A and m_B, and the coefficients of friction are μ_A and μ_B. If m_A = m_B=4.0kg, and μ_A = 0.20 and μ_B = 0.30, determine the acceleration of the blocks.

Two blocks made of different materials connected together by a thin cord slide down a ramp inclined at an angle θ to the horizontal, Fig. 5–40 (block B is above block A). The masses of the blocks are m_A and m_B, and the coefficients of friction are μ_A and μ_B. If m_A = m_B = 4.0kg, and μ_A = 0.20 and μ_B = 0.30, determine the tension in the cord, for an angle θ = 32°.

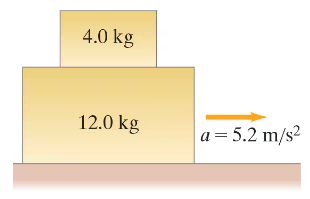
(III) A 4.0-kg block is stacked on top of a 12.0-kg block, which is accelerating along a horizontal table at a = 5.2m/s² (Fig. 5–43). Let μ_k = μ_s = μ. What is the force that must be applied to the 12.0-kg block in (a) and in (b), assuming that the table is frictionless?

A jet plane traveling 1890 km/h (525 m/s) pulls out of a dive by moving in an arc of radius 4.80 km. What is the plane's acceleration in g's?

On an ice rink two skaters of equal mass grab hands and spin in a mutual circle once every 2.5 s. If we assume their arms are each 0.80 m long and their individual masses are 55.0 kg, how hard are they pulling on one another?

Tarzan plans to cross a gorge by swinging in an arc from a hanging vine (Fig. 5–50). If his arms are capable of exerting a force of 1350 N on the vine, what is the maximum speed he can tolerate at the lowest point of his swing? His mass is 78 kg and the vine is 4.8 m long.

A pilot performs an evasive maneuver by diving vertically at a constant 310 m/s. If he can withstand an acceleration of 9.0 g’s without blacking out, at what altitude must he begin to pull his plane out of the dive (moving in a vertical circular path) to avoid crashing into the sea?

The position of a particle moving in the xy plane is given by $\overrightarrow{r}$ = (2.0m) cos [(3.0 rad/s)t ] $\hat{i}$ +(2.0m) sin [(3.0 rad/s)t ] $\hat{j}$, where r is in meters and t is in seconds. Calculate the velocity and acceleration vectors as functions of time.

A coffee cup on the horizontal dashboard of a car slides forward when the driver decelerates from 45 km/h to rest in 3.5 s or less, but not if she decelerates in a longer time. What is the coefficient of static friction between the cup and the dash? Assume the road and the dashboard are level (horizontal).

The 70.0-kg climber in Fig. 5–53 is supported in the 'chimney' by the friction forces exerted on his shoes and back. The static coefficients of friction between his shoes and the wall, and between his back and the wall, are 0.80 and 0.60, respectively. What is the minimum normal force he must exert? Assume the walls are vertical and that the static friction forces are both at their maximum. Ignore his grip on the rope.

A train traveling at a constant speed rounds a curve of radius 215 m. A lamp suspended from the ceiling swings out to an angle of 18.5° throughout the curve. What is the speed of the train? [Hint: See Example 4–15.]

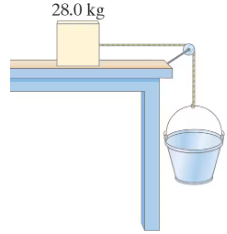
A 28.0-kg block is connected to an empty 2.00-kg bucket by a cord running over a frictionless pulley (Fig. 5–56). The coefficient of static friction between the table and the block is 0.42 and the coefficient of kinetic friction between the table and the block is 0.34. Sand is gradually added to the bucket until the system just begins to move. Calculate the acceleration of the system.

A car starts rolling down a 1-in-4 hill (1-in-4 means that for each 4 m traveled along the road, the elevation change is 1 m). How fast is it going when it reaches the bottom after traveling 55 m? Assume an effective coefficient of rolling friction equal to 0.10.

A 68-kg water skier is being accelerated by a ski boat on a flat ('glassy') lake. The coefficient of kinetic friction between the skier's skis and the water surface is μₖ = 0.25 (Fig. 5–59). What is the skier's acceleration if the rope pulling the skier behind the boat applies a horizontal tension force of magnitude F_T = 240N to the skier (θ = 0°)?

<IMAGE>

A 68-kg water skier is being accelerated by a ski boat on a flat ('glassy') lake. The coefficient of kinetic friction between the skier's skis and the water surface is μₖ = 0.25 (Fig. 5–59). What is the skier's horizontal acceleration if the rope pulling the skier exerts a force of F_T = 240N on the skier at an upward angle θ = 12°?

A 68-kg water skier is being accelerated by a ski boat on a flat ('glassy') lake. The coefficient of kinetic friction between the skier's skis and the water surface is μₖ = 0.25 (Fig. 5–59). Explain why the skier's acceleration in part (b) is greater than that in part (a).