Back
BackProblem 2
A delivery truck travels 21 blocks north, 16 blocks east, and 26 blocks south. What is its final displacement from the origin? Assume the blocks are equal length.
Problem 7a
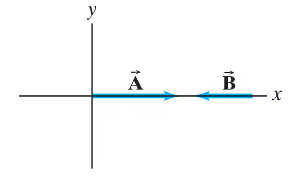
Figure 3–39 shows two vectors, and , whose magnitudes are A = 6.8 units and B = 5.5 units. Determine if = + . Give the magnitude and direction for each.
Problem 8a
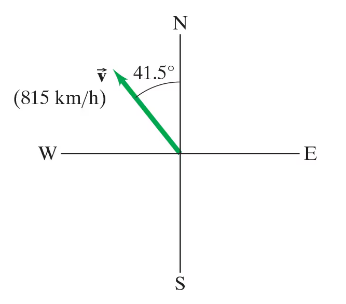
An airplane is traveling 815 km/h in a direction 41.5° west of north (Fig. 3–40). Find the components of the velocity vector in the northerly and westerly directions.
Problem 10
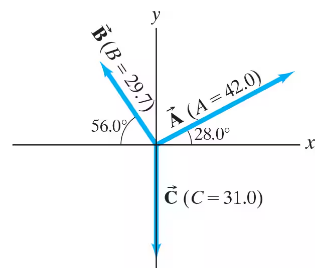
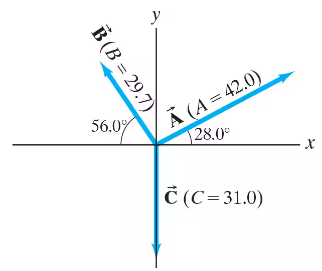
Three vectors are shown in Fig. 3–41. Their magnitudes are given in arbitrary units. Determine the sum of the three vectors. Give the resultant in terms of (a) components, (b) magnitude and angle with the +𝓍 axis.
Problem 13b
For the vectors shown in Fig. 3–41, determine 2 A - 3 B + 2 C.
Problem 17b
Two vectors, and , add to a resultant . Describe and if .
Problem 21
A car is moving with speed 16.0 m/s due south at one moment and 25.7 m/s due east 8.00 s later. Over this time interval, determine the magnitude and direction of (a) its average velocity, (b) its average acceleration. (c) What is its average speed? [Hint: Can you determine all these from the information given?]
Problem 23a
A skier is accelerating down a 30.0° hill at 1.80 m/s² (Fig. 3–42). What is the vertical component of her acceleration?
<IMAGE>
Problem 23b
A skier is accelerating down a 30.0° hill at 1.80 m/s² (Fig. 3–42). How long will it take her to reach the bottom of the hill, assuming she starts from rest and accelerates uniformly, if the elevation change is 125 m?
<IMAGE>
Problem 33
A diver running 2.5 m/s dives out horizontally from the edge of a vertical cliff and 3.5 s later reaches the water below. How high was the cliff and how far from its base did the diver hit the water?
Problem 45a
A stunt driver wants to make his car jump over 8 cars parked side by side below a horizontal ramp (Fig. 3–46). With what minimum speed must he drive off the horizontal ramp? The vertical height of the ramp is 1.5 m above the car roofs and the horizontal distance he must clear is 22 m.
<IMAGE>
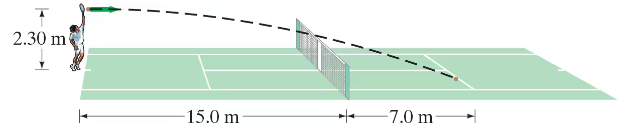
Problem 56
At serve, a tennis player aims to hit the ball horizontally. What minimum speed is required for the ball to clear the 0.90-m-high net about 15.0 m from the server if the ball is 'launched' from a height of 2.30 m? Where will the ball land if it just clears the net (and will it be 'good' in the sense that it lands within 7.0 m of the net)? How long will it be in the air? See Fig. 3–50.
Problem 65b
A motorboat whose speed in still water is 4.30 m/s must aim upstream at an angle of 23.5° (with respect to a line perpendicular to the shore) in order to travel directly across the stream. What is the resultant speed of the boat with respect to the shore? (See Fig. 3–33.)
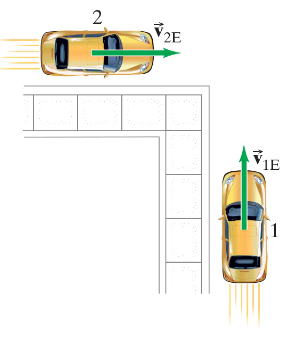
Problem 73a
Two cars approach a street corner at right angles to each other (Fig. 3–57). Car 1 travels at a speed relative to Earth v₁ₑ = 35 km/h, and car 2 at v₂ₑ = 55 km/h. What is the relative velocity of car 1 as seen by car 2? What is the velocity of car 2 relative to car 1?
Problem 92b
A person in the passenger basket of a hot-air balloon throws a ball horizontally outward from the basket with speed 12.0 m/s (Fig. 3–64). What initial velocity (magnitude and direction) does the ball have relative to a person standing on the ground if the hot-air balloon is descending at 3.0 m/s relative to the ground?
<IMAGE>