If you are driving 85 km/h along a straight road and you look to the side for 2.0 s, how far do you travel during this inattentive period?

A particle at t₁ = ― 2.0 s is at 𝓍₁ = 5.2 cm and at t₂ = 3.4 s is at 𝓍₂ = 8.5 cm. What is its average velocity over this time interval? Can you calculate its average speed from these data? Why or why not?

A horse trots away from its trainer in a straight line, moving 38 m away in 7.4 s. It then turns abruptly and gallops halfway back in 1.8 s. Calculate its average speed

Every year the Earth travels about 10⁹ km as it orbits the Sun. What is Earth's average speed in km/h?

An airplane travels 1900 km at a speed of 720 km/h, and then encounters a tailwind that boosts its speed to 990 km/h for the next 2700 km. What was the total time for the trip? What was the average speed of the plane for this trip? [Hint: Does Eq. 2–12d apply?]

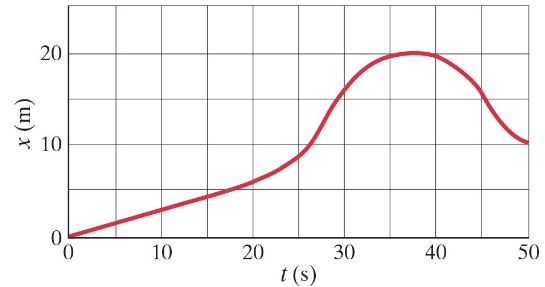
The position of an object along a straight tunnel as a function of time is plotted in Fig. 2–40. What is its average velocity between t = 25.0 s and t = 30.0 s?

Sketch the v vs. t graph for the object whose displacement as a function of time is given by Fig. 2–40.

A bowling ball traveling with constant speed hits the pins at the end of a bowling lane 16.5 m long. The bowler hears the sound of the ball hitting the pins 2.75 s after the ball is released from his hands. What is the speed of the ball, assuming the speed of sound is 340 m/s?

The position of an object is given by 𝓍 = At + Bt², where 𝓍 is in meters and t is in seconds. What are the units of A and B?

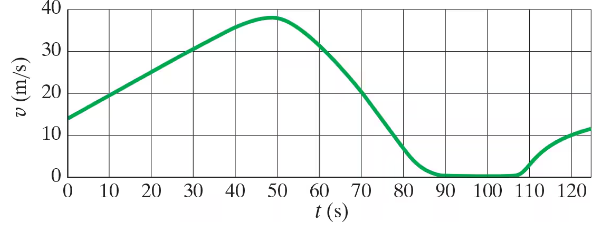
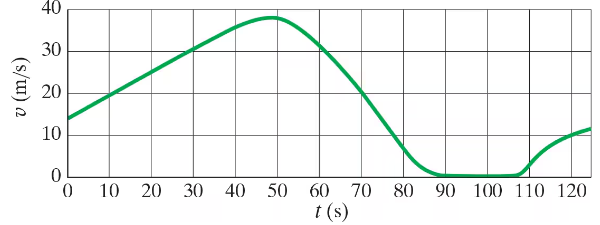
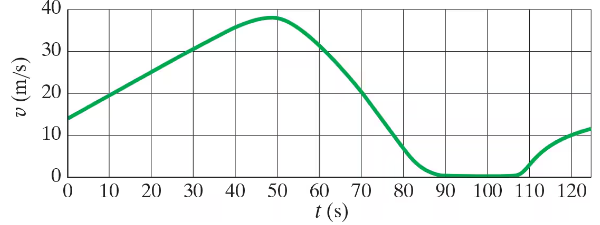
Figure 2–42 shows the velocity of a train as a function of time. At what time was its velocity greatest?

Figure 2–42 shows the velocity of a train as a function of time. During what periods, if any, was the velocity constant?

Figure 2–42 shows the velocity of a train as a function of time. During what periods, if any, was the acceleration constant?

A baseball pitcher throws a baseball with a speed of 43 m/s. Estimate the average acceleration of the ball during the throwing motion. In throwing the baseball, the pitcher accelerates it through a displacement of about 3.5 m, from behind the body to the point where it is released (Fig. 2–44).

<IMAGE>

A car traveling 85 km/h slows down at a constant 0.50 m/s² just by 'letting up on the gas.' Calculate the distance it travels during the first and fifth seconds.

For an object falling freely from rest, show that the distance traveled during each successive second increases in the ratio of successive odd integers (1, 3, 5, etc.). (This was first shown by Galileo.) See Figs. 2–27 and 2–30.

A rocket rises vertically, from rest, with an acceleration of 3.2 m/s² until it runs out of fuel at an altitude of 725 m. After this point, its acceleration is that of gravity, downward. What maximum altitude does the rocket reach?

A helicopter is ascending vertically with a constant speed of 6.40 m/s. At a height of 105 m above the Earth, a package is dropped from the helicopter. How much time does it take for the package to reach the ground? [Hint: What is v₀ for the package?]

Roger sees water balloons fall past his window. He notices that each balloon strikes the sidewalk 0.83 s after passing his window, 15 m above the sidewalk. Assuming the balloons are being released from rest, from what height are they being released?

A baseball is seen to pass upward by a window with a vertical speed of 13 m/s. If the ball was thrown by a person 18 m below on the street, when was it thrown?

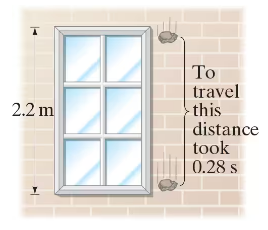
A falling stone takes 0.28 s to travel past a window 2.2 m tall (Fig. 2–49). From what height above the top of the window did the stone fall?

Air resistance acting on a falling body can be taken into account by the approximate relation for the acceleration: a = dv/dt = g ― kv, where k is a constant. Determine an expression for the terminal velocity, which is the maximum value the velocity reaches.

The position of a ball rolling in a straight line is given by 𝓍 = 2.0 ― 3.6t + 1.7t², where 𝓍 is in meters and t in seconds. What do the numbers 2.0, 3.6, and 1.7 refer to?

A police car at rest is passed by a speeder traveling at a constant 140 km/h. The police officer takes off in hot pursuit and catches up to the speeder in 850 m, maintaining a constant acceleration. Qualitatively plot the position vs. time graph for both cars from the police car's start to the catch-up point.

Two children are playing on two trampolines. The first child bounces up one-and-a-half times higher than the second child. The initial speed upwards of the second child is 4.0 m/s. What is the initial speed of the first child?

Suppose a 65-kg person jumps from a height of 3.0 m down to the ground. What is the speed of the person just before landing (Chapter 2)?

<IMAGE>

A parachutist bails out of an airplane, and freely falls 75 m (ignore air friction). Then the parachute opens, and her acceleration is ― 1.5 m/s² (up). The parachutist reaches the ground with a speed of 1.5 m/s. From how high did she bail out of the plane?

A robot used in a pharmacy picks up a medicine bottle at t = 0. It accelerates at 0.20 m/s² for 4.5 s, then travels without acceleration for 68 s and finally decelerates at ―0.40 m/s² for 2.5 s to reach the counter where the pharmacist will take the medicine from the robot. From how far away did the robot fetch the medicine?

Bill can throw a ball vertically at a speed 1.5 times faster than Joe can. How many times higher will Bill's ball go than Joe's?

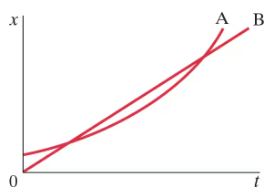
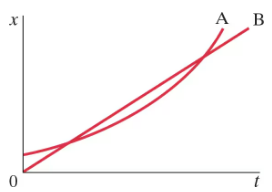
Figure 2–55 shows the position vs. time graph for two bicycles, A and B. At which instant(s) are the bicycles passing each other? Which bicycle is passing the other?

Figure 2–55 shows the position vs. time graph for two bicycles, A and B. Which bicycle has the larger average velocity?