Carbon dioxide makes up approximately 0.04% of Earth’s atmosphere. If you collect a 2.0-L sample from the atmosphere at sea level (1.00 atm) on a warm day (27°C), how many CO2 molecules are in your sample?

Verified step by step guidance

Convert the percentage of CO2 in the atmosphere to a decimal by dividing by 100. For CO2, this is 0.04%, which becomes 0.0004 when converted.

Use the ideal gas law, PV = nRT, to find the number of moles of gas in the sample. Rearrange the formula to solve for n (number of moles): n = \frac{PV}{RT}.

Substitute the values into the ideal gas law equation, using P = 1.00 atm, V = 2.0 L, R = 0.0821 L\cdot atm/(mol\cdot K), and T = 300 K (which is 27°C converted to Kelvin by adding 273).

Calculate the total moles of air in the sample, and then use the decimal fraction of CO2 to find the moles of CO2. Multiply the total moles by 0.0004.

Convert the moles of CO2 to molecules by using Avogadro's number (6.022 \times 10^{23} molecules/mol). Multiply the moles of CO2 by Avogadro's number to find the number of CO2 molecules.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

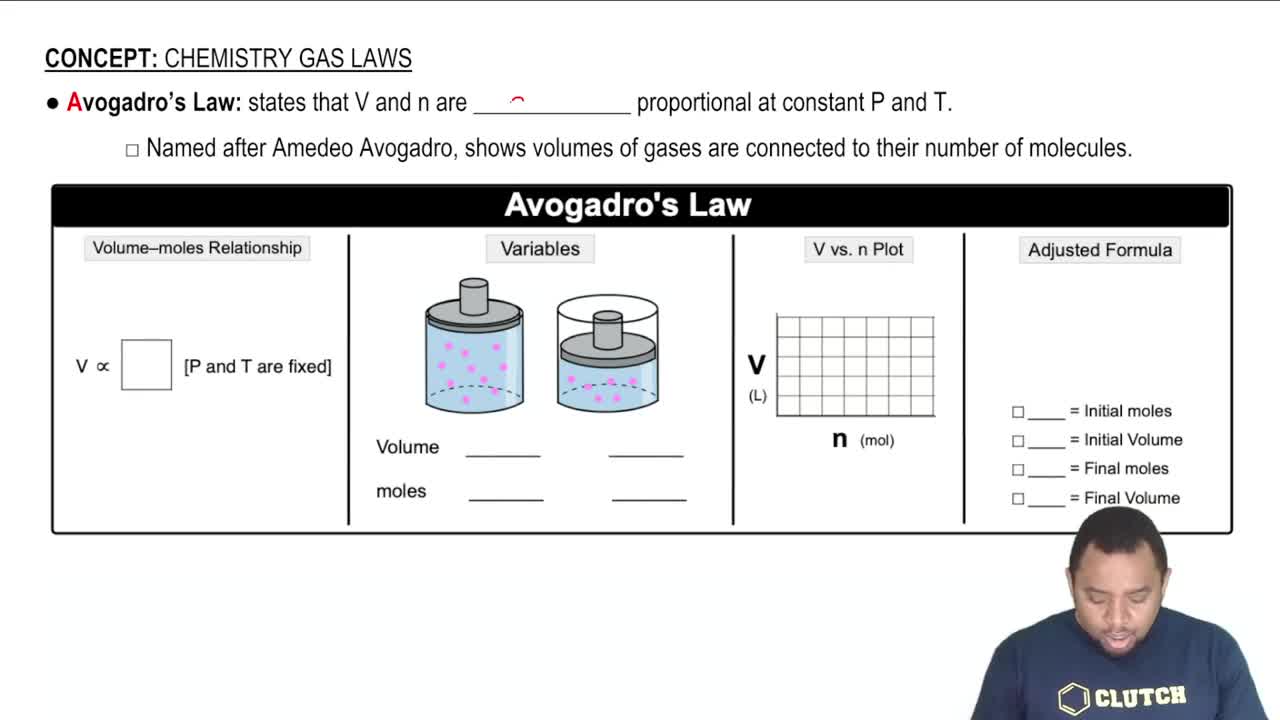
Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Ideal Gas Law

The Ideal Gas Law relates the pressure, volume, temperature, and number of moles of a gas through the equation PV = nRT. This law allows us to calculate the number of moles of a gas when its pressure, volume, and temperature are known, which is essential for determining the number of molecules in a sample.

Avogadro's Number

Avogadro's Number, approximately 6.022 x 10²³, is the number of particles (atoms, molecules, etc.) in one mole of a substance. This concept is crucial for converting moles of a gas, calculated using the Ideal Gas Law, into the actual number of molecules present in the sample.

Molar Volume of a Gas

At standard temperature and pressure (STP), one mole of an ideal gas occupies 22.4 liters. However, at different conditions, such as the given temperature and pressure, the molar volume can vary. Understanding how to adjust for these conditions is important for accurately calculating the number of molecules in a gas sample.

Recommended video:

Guided course

00:51

The Ideal Gas Law: Molar Mass

Related Practice

Textbook Question

Calculate the number of molecules in a deep breath of air whose volume is 2.25 L at body temperature, 37°C, and a pressure of 735 torr.

Textbook Question

The adult blue whale has a lung capacity of 5.0×103 L. Calculate the mass of air (assume an average molar mass of 28.98 g/mol) contained in an adult blue whale’s lungs at 0.0°C and 1.00 atm, assuming the air behaves ideally.

Textbook Question

If the pressure exerted by ozone, O3, in the stratosphere is 3.0×10−3atm and the temperature is 250 K, how many ozone molecules are in a liter?

Textbook Question

A scuba diver’s tank contains 0.29 kg of O2 compressed into a volume of 2.3 L. b. What volume would this oxygen occupy at 26°C and 0.95 atm?

Textbook Question

An aerosol spray can with a volume of 250 mL contains 2.30 g of propane gas (C3H8) as a propellant. a. If the can is at 23°C, what is the pressure in the can?

Textbook Question

An aerosol spray can with a volume of 250 mL contains 2.30 g of propane gas (C3H8) as a propellant. c. The can’s label says that exposure to temperatures above 130°F may cause the can to burst. What is the pressure in the can at this temperature?