Textbook Question
Calculate the percent ionization of propionic acid (C2H5COOH) in solutions of each of the following concentrations (Ka is given in Appendix D): (a) 0.250 M (b) 0.0800 M (c) 0.0200 M

 Verified step by step guidance
Verified step by step guidance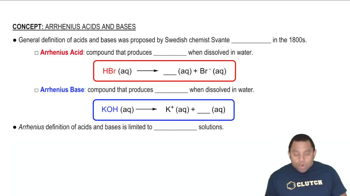


Calculate the percent ionization of propionic acid (C2H5COOH) in solutions of each of the following concentrations (Ka is given in Appendix D): (a) 0.250 M (b) 0.0800 M (c) 0.0200 M
Citric acid, which is present in citrus fruits, is a triprotic acid (Table 16.3). (a) Calculate the pH of a 0.040 M solution of citric acid. (b) Did you have to make any approximations or assumptions in completing your calculations? (c) Is the concentration of citrate ion 1C6H5O7 3-2 equal to, less than, or greater than the H+ ion concentration?
Consider the base hydroxylamine, NH2OH. (a) What is the conjugate acid of hydroxylamine?
The hypochlorite ion, ClO-, acts as a weak base. (a) Is ClO- a stronger or weaker base than hydroxylamine?