Textbook Question
Write the chemical equation and the Kb expression for the reaction of each of the following bases with water: (c) benzoate ion, C6H5CO2-

 Verified step by step guidance
Verified step by step guidance

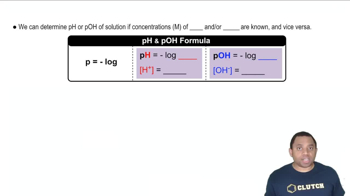
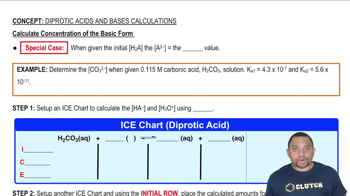
Write the chemical equation and the Kb expression for the reaction of each of the following bases with water: (c) benzoate ion, C6H5CO2-
Ephedrine, a central nervous system stimulant, is used in nasal sprays as a decongestant. This compound is a weak organic base: C10H15ON1aq2 + H2O1l2 Δ C10H15ONH+1aq2 + OH-1aq2 A 0.035 M solution of ephedrine has a pH of 11.33. (b) Calculate Kb for ephedrine.
Codeine 1C18H21NO32 is a weak organic base. A 5.0 * 10-3M solution of codeine has a pH of 9.95. Calculate the value of Kb for this substance. What is the pKb for this base?