Molecular iodine, I2(g), dissociates into iodine atoms at 625 K with a first-order rate constant of 0.271 s-1. (b) If you start with 0.050 M I2 at this temperature, how much will remain after 5.12 s assuming that the iodine atoms do not recombine to form I2?

Verified step by step guidance

Identify the type of reaction: The problem states that the dissociation of I2 is a first-order reaction. This means the rate of reaction depends linearly on the concentration of I2.

Use the first-order rate equation: The integrated rate law for a first-order reaction is given by \( [A]_t = [A]_0 e^{-kt} \), where \([A]_t\) is the concentration at time \(t\), \([A]_0\) is the initial concentration, \(k\) is the rate constant, and \(t\) is the time.

Substitute the known values into the equation: Here, \([A]_0 = 0.050\) M, \(k = 0.271\) s\(^{-1}\), and \(t = 5.12\) s. Substitute these values into the equation to find \([A]_t\).

Calculate the exponent: Compute \(-kt\) using the given values of \(k\) and \(t\).

Solve for \([A]_t\): Use the calculated exponent to find \([A]_t\) by evaluating the expression \( [A]_t = [A]_0 e^{-kt} \). This will give you the concentration of I2 remaining after 5.12 seconds.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

First-Order Kinetics

First-order kinetics refers to a reaction rate that is directly proportional to the concentration of one reactant. In this case, the dissociation of molecular iodine (I2) into iodine atoms follows first-order kinetics, meaning the rate of reaction can be expressed using the equation: rate = k[I2], where k is the rate constant. This concept is crucial for determining how the concentration of I2 changes over time.

Integrated Rate Law

The integrated rate law for a first-order reaction is given by the equation: ln([A]0/[A]) = kt, where [A]0 is the initial concentration, [A] is the concentration at time t, k is the rate constant, and t is time. This equation allows us to calculate the remaining concentration of I2 after a specific time period, which is essential for solving the problem presented.

Half-Life of a Reaction

The half-life of a reaction is the time required for the concentration of a reactant to decrease to half of its initial value. For first-order reactions, the half-life is constant and independent of concentration, calculated using the formula t1/2 = 0.693/k. Understanding half-life can provide insight into the time scale of the reaction and help in estimating how much I2 remains after a given time.

Recommended video:

Guided course

01:49

First-Order Half-Life

Related Practice

Textbook Question

The decomposition of sodium bicarbonate (baking soda), NaHCO₃(s), into Na₂CO₃(s), H₂O(l), and CO₂(g) at constant pressure requires the addition of 85 kJ of heat per two moles of NaHCO₃. (b) Draw an enthalpy diagram for the reaction.

Textbook Question

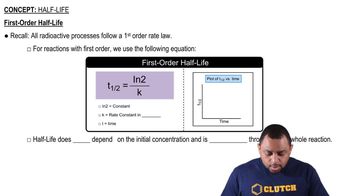
(a) The gas-phase decomposition of SO₂Cl₂, SO₂Cl₂(g) → SO₂(g) + Cl₂(g), is first order in SO₂Cl₂. At 600 K the half-life for this process is 2.3 × 10⁵ s. What is the rate constant at this temperature?

views

Textbook Question

(b) At 320°C the rate constant is 2.2 × 10^-5 s^-1. What is the half-life at this temperature?

Textbook Question

As described in Exercise 14.41, the decomposition of sulfuryl chloride (SO₂Cl₂) is a first-order process. The rate constant for the decomposition at 660 K is 4.5 × 10^-2 s^-1. (a) If we begin with an initial SO₂Cl₂ pressure of 450 torr, what is the partial pressure of this substance after 60 s?

Textbook Question

As described in Exercise 14.41, the decomposition of sulfuryl chloride (SO₂Cl₂) is a first-order process. The rate constant for the decomposition at 660 K is 4.5 × 10^-2 s^-1. (b) At what time will the partial pressure of SO₂Cl₂ decline to one-tenth its initial value?