Textbook Question
The reaction 2 NO(g) + O2(g) → 2 NO2 (g) is second order in NO and first order in O2. When [NO] = 0.040 M, and [O2] = 0.035 M, the observed rate of disappearance of NO is 9.3⨉10-5 M/s. (c) What are the units of the rate constant?
Ch.14 - Chemical Kinetics
Chapter 14, Problem 93b,c
Consider the following reaction between mercury(II) chloride and oxalate ion:
2 HgCl2(aq) + C2O42-(aq) → 2 Cl-(aq) + 2 CO2(g) + Hg2Cl2(s)
The initial rate of this reaction was determined for several concentrations of HgCl2 and C2O42-, and the following rate data were obtained for the rate of disappearance of C2O42-:
Experiment [HgCl2] (M) [C2O42-] (M) Rate (M/s)
1 0.164 0.15 3.2 × 10-5
2 0.164 0.45 2.9 × 10-4
3 0.082 0.45 1.4 × 10-4
4 0.246 0.15 4.8 × 10-5
(b) What is the value of the rate constant with proper units?
(c) What is the reaction rate when the initial concentration of HgCl2 is 0.100 M and that of C2O42- is 0.25 M if the temperature is the same as that used to obtain the data shown?
Verified step by step guidance1
Identify the rate law expression for the reaction. The general form is: \( \text{Rate} = k [\text{HgCl}_2]^m [\text{C}_2\text{O}_4^{2-}]^n \), where \( k \) is the rate constant, and \( m \) and \( n \) are the reaction orders with respect to \( \text{HgCl}_2 \) and \( \text{C}_2\text{O}_4^{2-} \), respectively.
Use the experimental data to determine the reaction orders \( m \) and \( n \). Compare experiments where only one concentration changes while the other remains constant to find \( m \) and \( n \).
Calculate the rate constant \( k \) using the rate law and data from one of the experiments once \( m \) and \( n \) are known.
Substitute the given concentrations \([\text{HgCl}_2] = 0.100 \text{ M}\) and \([\text{C}_2\text{O}_4^{2-}] = 0.25 \text{ M}\) into the rate law expression.
Calculate the reaction rate using the determined rate constant \( k \) and the substituted concentrations.
Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
4mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rate of Reaction
The rate of a chemical reaction is a measure of how quickly reactants are converted into products. It can be expressed in terms of the change in concentration of a reactant or product over time. Understanding the rate is crucial for predicting how changes in concentration affect the speed of the reaction, which is essential for solving the given problem.
Recommended video:
Guided course
02:03
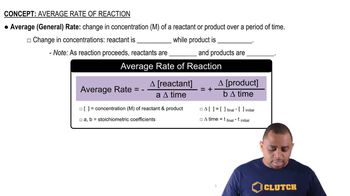
Average Rate of Reaction
Rate Law
The rate law is an equation that relates the rate of a reaction to the concentration of its reactants, typically expressed as rate = k[A]^m[B]^n, where k is the rate constant, and m and n are the orders of the reaction with respect to reactants A and B. Determining the rate law from experimental data allows us to predict the reaction rate under different concentrations, which is necessary for answering the question.
Recommended video:
Guided course
01:52Rate Law Fundamentals
Concentration and Reaction Order
Concentration refers to the amount of a substance in a given volume, and it significantly influences the rate of a reaction. The reaction order indicates how the rate is affected by the concentration of each reactant. By analyzing the provided data, one can deduce the reaction order for HgCl2 and C2O4 2-, which is essential for calculating the reaction rate at new concentrations.
Recommended video:
Guided course
02:44Zero-Order Reactions
Related Practice
Textbook Question
The reaction 2 NO(g) + O2(g) → 2 NO2 (g) is second order in NO and first order in O2. When [NO] = 0.040 M, and [O2] = 0.035 M, the observed rate of disappearance of NO is 9.3⨉10-5 M/s. (d) What would happen to the rate if the concentration of NO were increased by a factor of 1.8?
Textbook Question
The reaction 2 NO2 → 2 NO + O2 has the rate constant k = 0.63 M-1s-1. (a) Based on the units for k, is the reaction first or second order in NO2?
Textbook Question
The reaction 2 NO2 → 2 NO + O2 has the rate constant k = 0.63 M-1s-1.
(b) If the initial concentration of NO2 is 0.100 M, how would you determine how long it would take for the concentration to decrease to 0.025 M?