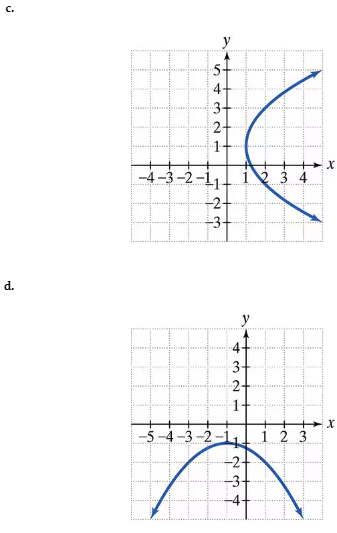
Find the vertex, focus, and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d). (y - 1)² = 4(x - 1)

a. b. c. d.

Find the standard form of the equation of each hyperbola.

Find the standard form of the equation of each ellipse satisfying the given conditions. Major axis horizontal with length 8; length of minor axis = 4; center: (0, 0)

Find the standard form of the equation of each ellipse satisfying the given conditions. Major axis vertical with length 10; length of minor axis = 4; center: (-2, 3)

Use the center, vertices, and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes. (x+4)²/9−(y+3)²/16=1

Find the vertex, focus, and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d). (x + 1)² = - 4(y + 1)

a. b. c. d.

In Exercises 31–34, find the vertex, focus, and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d). (y - 1)² = - 4(x - 1)

Find the vertex, focus, and directrix of each parabola with the given equation. Then graph the parabola. (x - 2)² = 8(y - 1)

Use the center, vertices, and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes. (x+3)²/25−y²/16=1

Find the vertex, focus, and directrix of the parabola with the given equation. Then graph the parabola. y^2 = 8x

Find the vertex, focus, and directrix of each parabola with the given equation. Then graph the parabola. (x + 1)² = - 8(y + 1)

Use the center, vertices, and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes. (y+2)²/4−(x−1)²/16=1

Graph each ellipse and give the location of its foci. (x − 2)²/9 + (y -1)² /4= 1

Find the vertex, focus, and directrix of the parabola with the given equation. Then graph the parabola. (y-2)^2 = -16x

Find the vertex, focus, and directrix of each parabola with the given equation. Then graph the parabola. (y + 3)² = 12(x + 1)

Use the center, vertices, and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes. (x−3)²−4(y+3)²=4

Graph each ellipse and give the location of its foci. (x +3)²+ 4(y -2)² = 16

Find the vertex, focus, and directrix of the parabola with the given equation. Then graph the parabola. (x-4)^2 = 4(y+1)

Find the vertex, focus, and directrix of the parabola with the given equation. Then graph the parabola. x^2 - 4x - 2y = 0

Use the center, vertices, and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes. (x−1)²−(y−2)²=3

Find the standard form of the equation of the parabola satisfying the given conditions. Focus: (12,0); Directrix: x=-12

Graph each ellipse and give the location of its foci. (x − 4)²/9 + (y +2)² /25= 1

Find the vertex, focus, and directrix of each parabola with the given equation. Then graph the parabola. (y + 1)² = - 8x

Find the standard form of the equation of the parabola satisfying the given conditions. Focus: (0,-11); Directrix: y=11

Convert each equation to standard form by completing the square on x and y. Then graph the hyperbola. Locate the foci and find the equations of the asymptotes. $x^2-y^2-2x-4y-4=0$

Convert each equation to standard form by completing the square on x or y. Then find the vertex, focus, and directrix of the parabola. Finally, graph the parabola. x² - 2x - 4y + 9 =0

Graph each ellipse and give the location of its foci. x²/25 + (y -2)² /36= 1

In Exercises 43–50, convert each equation to standard form by completing the square on x and y. Then graph the hyperbola. Locate the foci and find the equations of the asymptotes. $16x^2-y^2+64x-2y+67=0$

Convert each equation to standard form by completing the square on x or y. Then find the vertex, focus, and directrix of the parabola. Finally, graph the parabola. y² - 2y + 12x - 35 = 0

Graph each ellipse and give the location of its foci. (x +3)²/9 + (y -2)² = 1