Find the coordinates of the vertex for the parabola defined by the given quadratic function. f(x)=2x²−8x+3

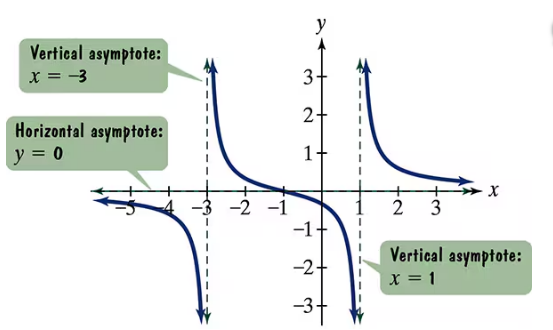
Use the graph of the rational function in the figure shown to complete each statement in Exercises 9–14.

As $x\to -\infty ,f\left(x\right){\to }_{{}_{}}$_____

In Exercises 9–16, a) List all possible rational zeros. b) Use synthetic division to test the possible rational zeros and find an actual zero. c) Use the quotient from part (b) to find the remaining zeros of the polynomial function. $f\left(x\right)=x^3+4x^2-3x-6$

In Exercises 1–16, divide using long division. State the quotient, and the remainder, r(x). (6x³+13x²−11x−15)/(3x²−x−3)

Divide using long division. State the quotient, and the remainder, r(x). (x⁴+2x³−4x²−5x−6)/(x²+x−2)

Solve each polynomial inequality in Exercises 1–42 and graph the solution set on a real number line. Express each solution set in interval notation. 6x²+x>1

In Exercises 9–16, a) List all possible rational zeros. b) Use synthetic division to test the possible rational zeros and find an actual zero. c) Use the quotient from part (b) to find the remaining zeros of the polynomial function. f(x)=2x³+x²−3x+1

Write an equation that expresses each relationship. Then solve the equation for y. x varies directly as the cube root of z and inversely as y.

Write an equation that expresses each relationship. Then solve the equation for y. x varies jointly as y and z and inversely as the square root of w.

In Exercises 15–18, use the Leading Coefficient Test to determine the end behavior of the graph of the given polynomial function. Then use this end behavior to match the polynomial function with its graph. [The graphs are labeled (a) through (d).] <IMAGE>

$f\left(x\right)=-x^4+x^2$

Find the coordinates of the vertex for the parabola defined by the given quadratic function. f(x)=−x²−2x+8

Use the graph of the rational function in the figure shown to complete each statement in Exercises 15–20.

As $x\to 1^{+},f\left(x\right)\to$ __

Find the zeros for each polynomial function and give the multiplicity of each zero. State whether the graph crosses the x-axis, or touches the x-axis and turns around, at each zero. $f\left(x\right)=-2(x-1)(x+2{)}^2(x+5{)}^3$

Divide using long division. State the quotient, and the remainder, r(x).$\frac{2x^5 - 8x^4 + 2x^3 + x^2}{2x^3 + 1}$

Solve each polynomial inequality in Exercises 1–42 and graph the solution set on a real number line. Express each solution set in interval notation.

Write an equation that expresses each relationship. Then solve the equation for y. x varies jointly as y and z and inversely as the square of w.

In Exercises 15–18, use the Leading Coefficient Test to determine the end behavior of the graph of the given polynomial function. Then use this end behavior to match the polynomial function with its graph. [The graphs are labeled (a) through (d).] <IMAGE>

$f\left(x\right)=(x-3{)}^2$

In Exercises 17–24, a) List all possible rational roots. b) List all possible rational roots. c) Use the quotient from part (b) to find the remaining roots and solve the equation. x³−2x²−11x+12=0

Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=(x−4)²−1

Write an equation that expresses each relationship. Then solve the equation for y. x varies jointly as z and the sum of y and w.

Solve each polynomial inequality in Exercises 1–42 and graph the solution set on a real number line. Express each solution set in interval notation. $5x\le 2-3x^2$

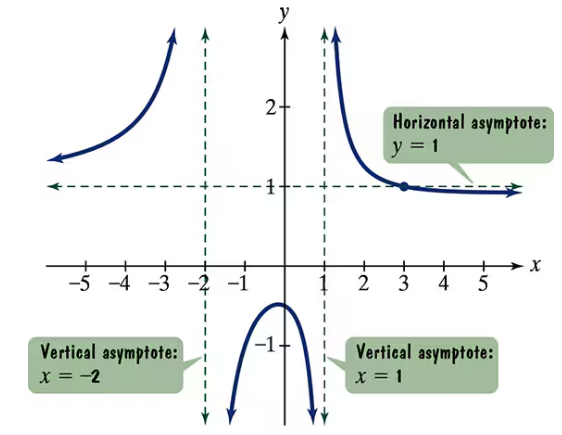
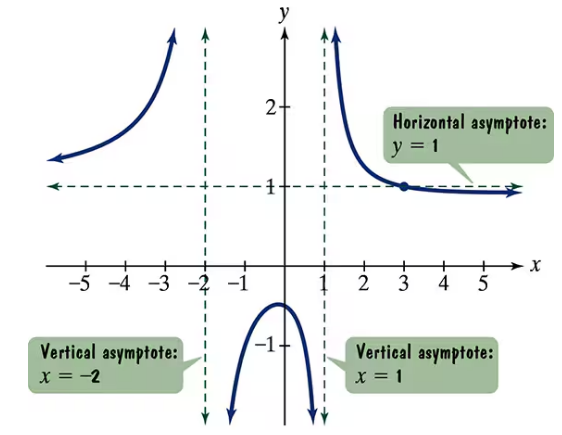
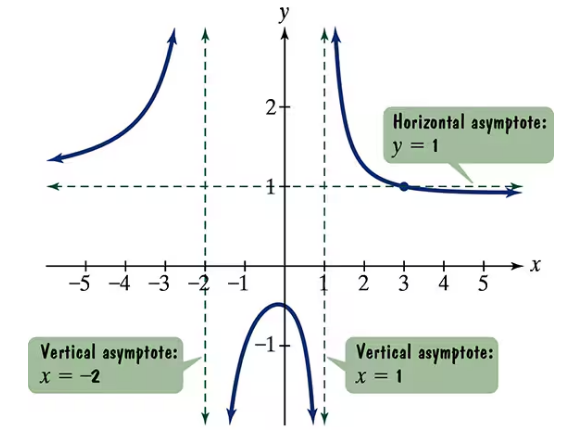
Use the graph of the rational function in the figure shown to complete each statement in Exercises 15–20.

As $x\to -2^{+},f\left(x\right)\to$ __

Divide using synthetic division. (2x²+x−10)÷(x−2)

Solve each polynomial inequality in Exercises 1–42 and graph the solution set on a real number line. Express each solution set in interval notation. 4x² + 1 ≥ 4x

Write an equation that expresses each relationship. Then solve the equation for y. x varies jointly as z and the difference between y and w.

Use the graph of the rational function in the figure shown to complete each statement in Exercises 15–20.

As $x\to \infty ,f\left(x\right)\to$_____

Solve each polynomial inequality in Exercises 1–42 and graph the solution set on a real number line. Express each solution set in interval notation. $x^2-4x\ge 0$

Use the vertex and intercepts to sketch the graph of each quadratic function. Give the equation of the parabola's axis of symmetry. Use the graph to determine the function's domain and range. f(x)=(x−1)²+2

In Exercises 17–24, a) List all possible rational roots. b) List all possible rational roots. c) Use the quotient from part (b) to find the remaining roots and solve the equation. x³−10x−12=0