Solve each equation. - 2{7 - [4 -2(1 - x) + 3]} = 10 - [4x - 2(x - 3)]

In Exercises 107–110, use graphs to find each set. (-2,1] ∩ [-1,3)

If 5 times a number is decreased by 4, the principal square root of this difference is 2 less than the number. Find the number(s).

When 3 times a number is subtracted from 4, the absolute value of the difference is at least 5. Use interval notation to express the set of all numbers that satisfy this condition.

Solve each equation in Exercises 83–108 by the method of your choice. 2x/(x - 3) + 6/(x + 3) = - 28/(x² - 9)

Solve each equation in Exercises 83–108 by the method of your choice. 3/(x - 3) + 5/(x - 4) = (x² - 20)/(x² - 7x + 12)

If a number is decreased by 3, the principal square root of this difference is 5 less than the number. Find the number(s).

When 4 times a number is subtracted from 5, the absolute value of the difference is at most 13. Use interval notation to express the set of all numbers that satisfy this condition.

In Exercises 107–110, use graphs to find each set. [1,3) ∩ (0,4)

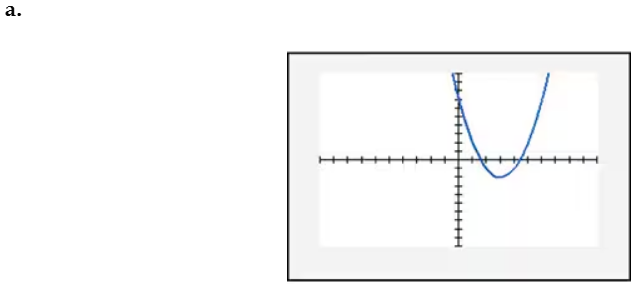
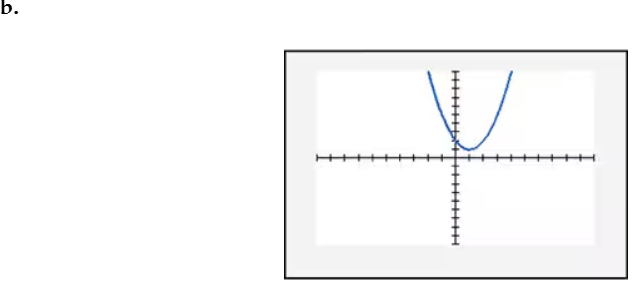
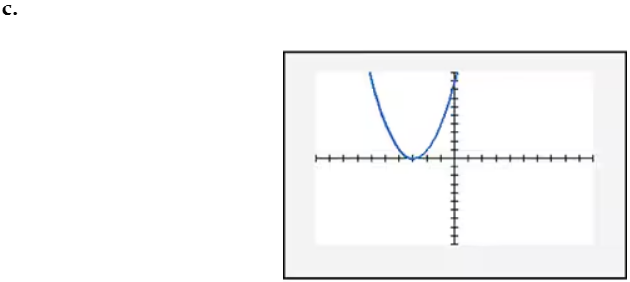
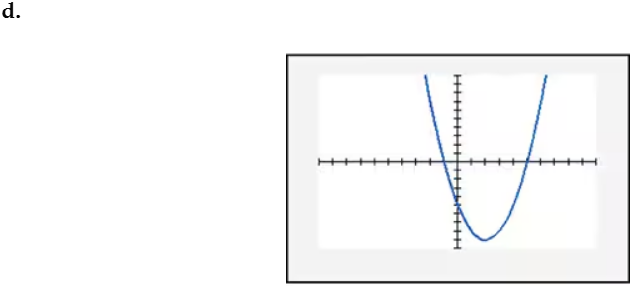
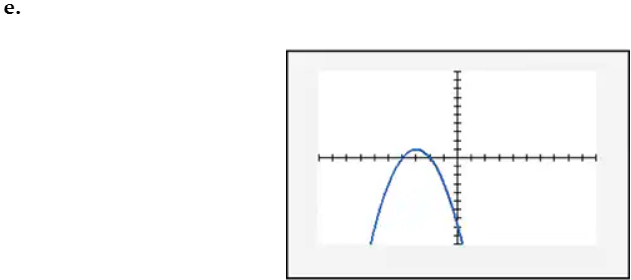
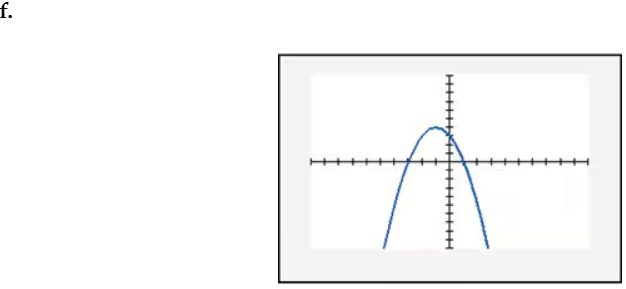
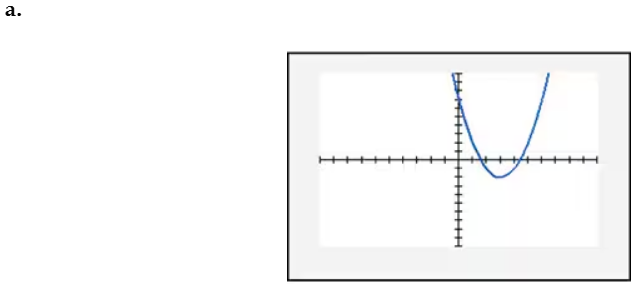
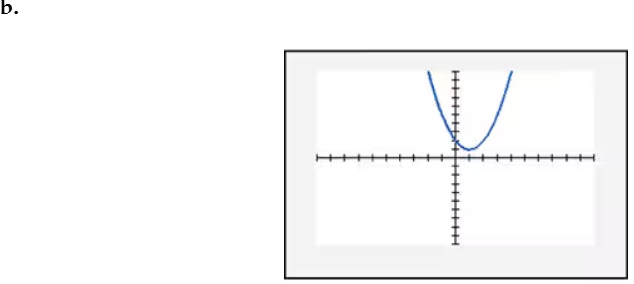
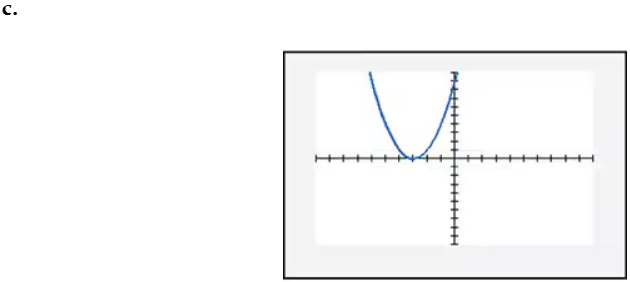
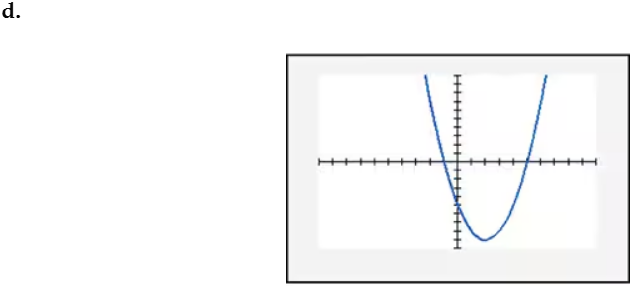
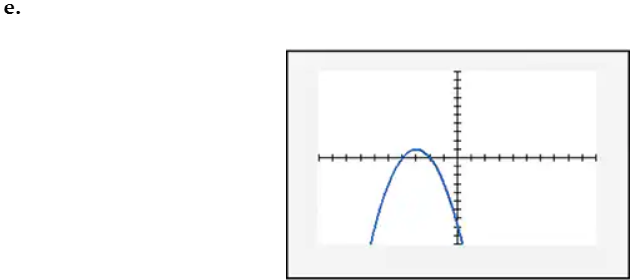
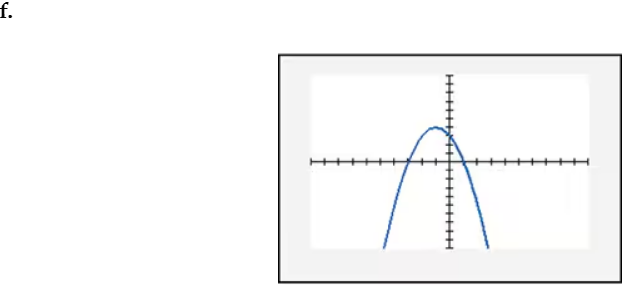
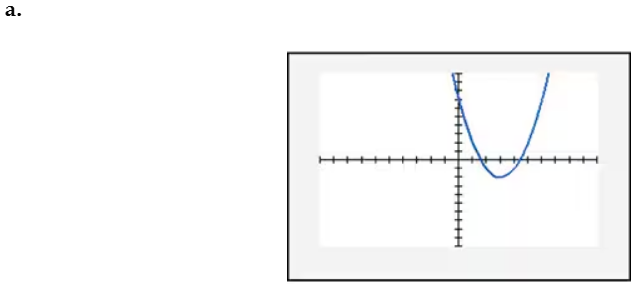
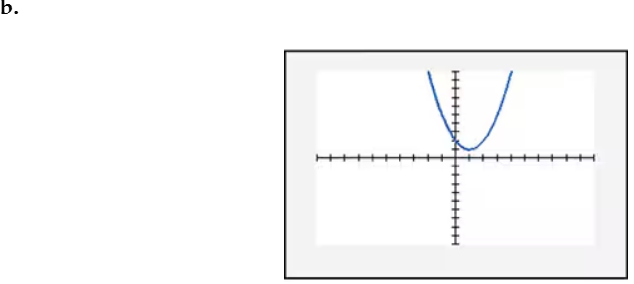
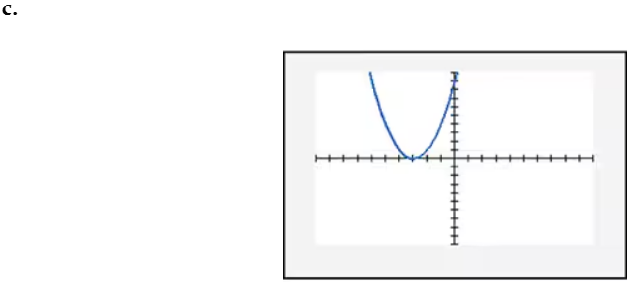
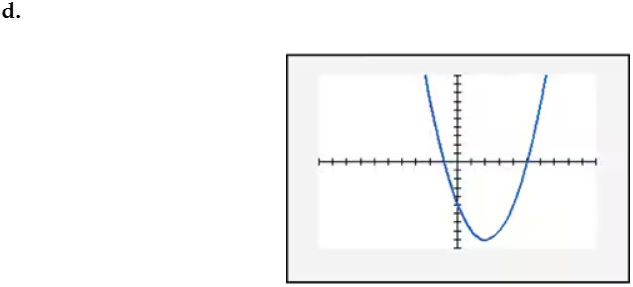
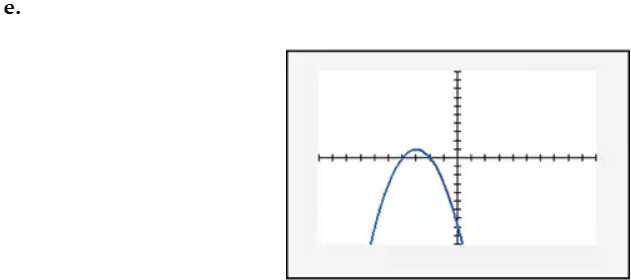
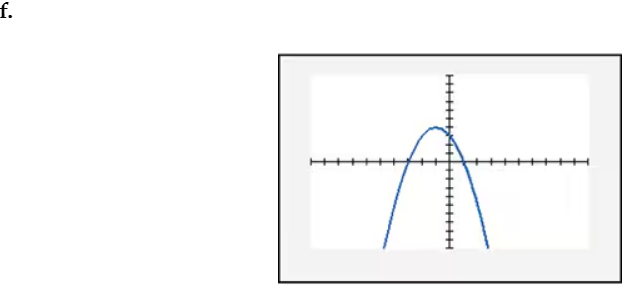
In Exercises 109–114, find the x-intercept(s) of the graph of each equation. Use the x-intercepts to match the equation with its graph. The graphs are shown in [- 10, 10, 1] by [- 10, 10, 1] viewing rectangles and labeled (a) through (f). y = x² - 4x - 5

Solve and graph the solution set on a number line: (2x−3)/4 ≥ 3x/4 + 1/2

In Exercises 109–114, find the x-intercept(s) of the graph of each equation. Use the x-intercepts to match the equation with its graph. The graphs are shown in [- 10, 10, 1] by [- 10, 10, 1] viewing rectangles and labeled (a) through (f). y = - (x + 1)² + 4

In Exercises 109–114, find the x-intercept(s) of the graph of each equation. Use the x-intercepts to match the equation with its graph. The graphs are shown in [- 10, 10, 1] by [- 10, 10, 1] viewing rectangles and labeled (a) through (f). y = x² - 2x + 2

Find all values of x satisfying the given conditions. y = 2x² - 3x and y = 2

Find all values of x satisfying the given conditions. y = 5x² + 3x and y = 2

Find all values of x satisfying the given conditions. y₁ = x - 1, y₂ = x + 4 and y₁y₂ = 14

Find all values of x satisfying the given conditions. y₁ = 2x/(x + 2), y₂ = 3/(x + 4), and y₁ + y₂ = 1

Find all values of x satisfying the given conditions. y₁ = 2x² + 5x - 4, y₂ = - x² + 15x - 10, and y₁ - y₂ = 0

Find all values of x satisfying the given conditions. y₁ = - x² + 4x - 2, y₂ = - 3x² + x - 1, and y₁ - y₂ = 0

What is an identity equation? Give an example.

List all numbers that must be excluded from the domain of each rational expression. 3/(2x² + 4x - 9)

What is a conditional equation? Give an example.

What is an inconsistent equation? Give an example.

When the sum of 6 and twice a positive number is subtracted from the square of the number, 0 results. Find the number.

When the sum of 1 and twice a negative number is subtracted from twice the square of the number, 0 results. Find the number.

Solve each equation by the method of your choice. 1/(x² - 3x + 2) = 1/(x + 2) + 5/(x² - 4)

Solve each equation by the method of your choice. √2 x² + 3x - 2√2 = 0

Find b such that (7x + 4)/b + 13 = x has a solution set given by {- 6}.

Find b such that (4x - b)/(x - 5) = 3 has a solution set given by {Ø}.

In Exercises 137–140, determine whether each statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement. The equation |x| = - 6 is equivalent to x = 6 or x = - 6.