Multiple Choice
A weatherman states that the probability that it will rain tomorrow is 10%, or 0.1, & the probability that it will snow is 25%, or 0.25. What is the probability that it will not rain or snow?
10. Combinatorics & Probability
Probability
Struggling with College Algebra?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
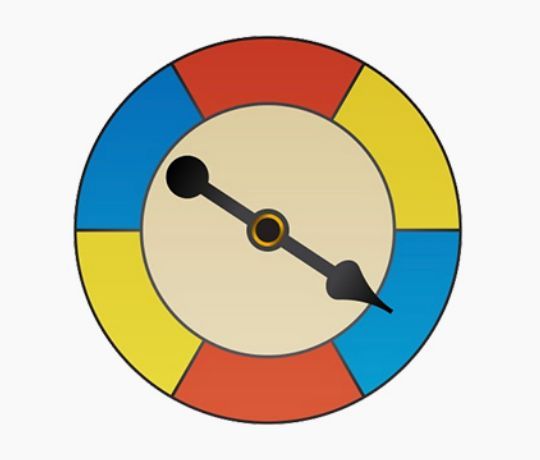
The spinner below has 6 equal regions. Find the probability of landing on yellow for the first spin and not landing on yellow on the second spin.
A
0.11
B
0.22
C
0.66
D
0.88
Verified step by step guidance1
First, identify the total number of regions on the spinner. In this case, there are 6 equal regions.
Next, count the number of yellow regions on the spinner. There are 2 yellow regions.
Calculate the probability of landing on yellow for the first spin. This is the number of yellow regions divided by the total number of regions: \( \frac{2}{6} \).
Now, calculate the probability of not landing on yellow on the second spin. There are 4 non-yellow regions, so the probability is \( \frac{4}{6} \).
To find the combined probability of both events (landing on yellow first and not landing on yellow second), multiply the probabilities of each event: \( \frac{2}{6} \times \frac{4}{6} \).
5:37mWatch next
Master Introduction to Probability with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
