If a single card is randomly selected from a deck of cards, what is the probability of selecting an ace or a king?
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
10. Combinatorics & Probability
Probability
Struggling with College Algebra?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
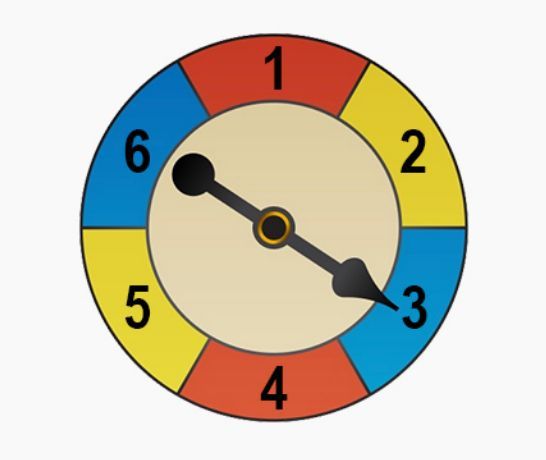
The spinner below has 6 equal colored regions numbered 1-6. Find the probability of stopping on yellow for the first spin, stopping on an even number on the second spin, and stopping on blue or red on the third spin.
A
0.11
B
0.17
C
0.50
D
0.89
 Verified step by step guidance
Verified step by step guidance1
Identify the total number of regions on the spinner, which is 6.
Determine the probability of stopping on yellow for the first spin. There are 2 yellow regions (numbered 2 and 5), so the probability is \( \frac{2}{6} \) or \( \frac{1}{3} \).
Determine the probability of stopping on an even number on the second spin. The even numbers are 2, 4, and 6, so there are 3 even numbers. The probability is \( \frac{3}{6} \) or \( \frac{1}{2} \).
Determine the probability of stopping on blue or red on the third spin. There are 2 blue regions (numbered 3 and 6) and 2 red regions (numbered 1 and 4), making a total of 4 regions. The probability is \( \frac{4}{6} \) or \( \frac{2}{3} \).
Multiply the probabilities of each independent event to find the overall probability: \( \frac{1}{3} \times \frac{1}{2} \times \frac{2}{3} \).

 5:37m
5:37mWatch next
Master Introduction to Probability with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice


