Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
Limits are fundamental in calculus, representing the value that a function approaches as the input approaches a certain point. In the context of rational functions, limits help determine the behavior of the function as the variable approaches infinity or negative infinity, which is crucial for understanding end behavior.
Recommended video:
Rational Functions
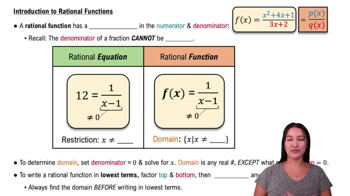
Rational functions are expressions formed by the ratio of two polynomials. The behavior of these functions as x approaches infinity or negative infinity can often be simplified by comparing the degrees of the numerator and denominator, which influences the limit's value.
Recommended video:
Intro to Rational Functions
End Behavior
End behavior refers to the behavior of a function as the input values become very large or very small. For rational functions, analyzing the leading coefficients and degrees of the numerator and denominator allows us to predict whether the limit will approach a finite number, infinity, or negative infinity.
Recommended video:
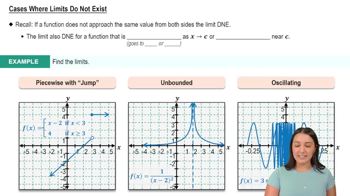
Cases Where Limits Do Not Exist
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 6:47m
6:47m