Here are the essential concepts you must grasp in order to answer the question correctly.
Limits at Infinity
Limits at infinity involve determining the behavior of a function as the input approaches positive or negative infinity. This concept helps in understanding the end behavior of functions, often simplifying expressions by focusing on dominant terms. For rational functions, this typically involves comparing the degrees of the numerator and denominator.
Recommended video:
Cases Where Limits Do Not Exist
Simplification of Rational Functions
Simplification of rational functions is crucial when finding limits at infinity. It involves identifying and focusing on the dominant terms in the numerator and denominator, as terms with higher powers of x will dictate the behavior of the function as x approaches infinity. This simplification often leads to easier computation of limits.
Recommended video:
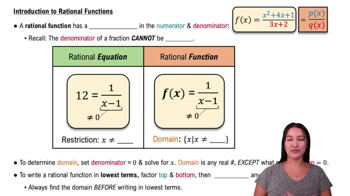
Intro to Rational Functions
Graphical Visualization
Graphical visualization aids in understanding the behavior of functions as x approaches infinity or negative infinity. By using graphing tools, one can observe the asymptotic behavior and confirm analytical results. This visual approach complements algebraic methods, providing a clearer picture of the function's end behavior.
Recommended video:
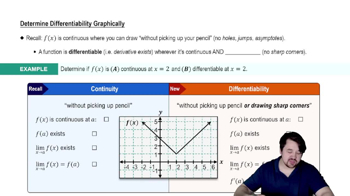
Determining Differentiability Graphically
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: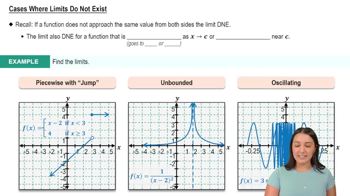

 6:47m
6:47m