Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
Limits are fundamental in calculus, representing the value that a function approaches as the input approaches a certain point. They are crucial for understanding the behavior of functions at specific points, including infinity. In this context, we are interested in evaluating the limits of the function g(x) as x approaches both positive and negative infinity.
Recommended video:
Behavior at Infinity
When analyzing limits as x approaches infinity or negative infinity, we focus on the end behavior of the function. This involves determining how the function behaves as the input grows larger or smaller without bound. For rational functions, this often involves simplifying the expression to identify dominant terms that dictate the limit.
Recommended video:
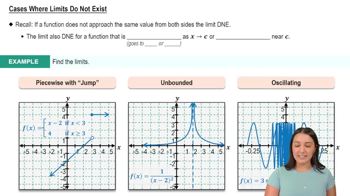
Cases Where Limits Do Not Exist
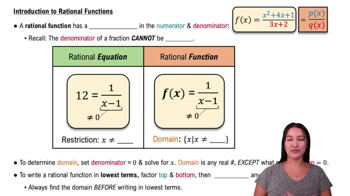
Rational Functions
Rational functions are ratios of polynomials, and their limits can often be evaluated by examining the degrees of the numerator and denominator. In the case of g(x) = 1/(2 + (1/x)), as x approaches infinity, the term (1/x) approaches zero, simplifying the function. Understanding how to manipulate and simplify rational functions is key to finding their limits.
Recommended video:
Intro to Rational Functions
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 6:47m
6:47m