113. If b, c, and d are constants, for what value of b will the curve y = x^3 + bx^2 + cx + d have a
point of inflection at x = 1? Give reasons for your answer.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: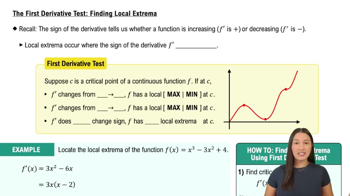


 6:38m
6:38mMaster Determining Concavity from the Graph of f with a bite sized video explanation from Patrick
Start learning