Textbook Question
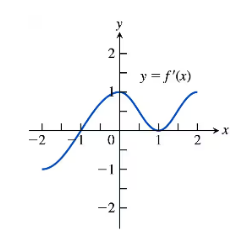
114. Parabolas
b. When is the parabola concave up? Concave down?
5. Graphical Applications of Derivatives
Concavity
2:39 minutesProblem 103
Textbook Question
103. A function f(x) has domain (-2, 2). The graph below is a plot of the derivative of f, not a plot of f itself. In other words, this is a graph of y = f'(x). Either use this graph to determine on which intervals the graph of f is concave up and on which intervals the graph of f is concave down, or explain why this information cannot be determined from the graph.
Verified step by step guidance1
To determine the concavity of the function f(x), we need to analyze the second derivative, f''(x). The graph provided is of the first derivative, f'(x).
The function f(x) is concave up where its second derivative, f''(x), is positive. This occurs where the graph of f'(x) is increasing.
Similarly, f(x) is concave down where its second derivative, f''(x), is negative. This occurs where the graph of f'(x) is decreasing.
From the graph, observe the intervals where f'(x) is increasing: this happens approximately from x = -2 to x = -1 and from x = 0 to x = 1. In these intervals, f(x) is concave up.
Observe the intervals where f'(x) is decreasing: this happens approximately from x = -1 to x = 0 and from x = 1 to x = 2. In these intervals, f(x) is concave down.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Concavity
Concavity refers to the direction in which a curve bends. A function is concave up on an interval if its second derivative is positive, indicating that the slope of the tangent line is increasing. Conversely, a function is concave down if its second derivative is negative, meaning the slope of the tangent line is decreasing. Understanding concavity helps in analyzing the behavior of the function's graph.
Recommended video:
05:59
Determining Concavity Given a Function
First Derivative Test
The first derivative test involves analyzing the sign of the derivative of a function to determine where the function is increasing or decreasing. If the derivative is positive, the function is increasing; if negative, it is decreasing. This information is crucial for understanding the behavior of the function and can indirectly provide insights into its concavity when combined with the second derivative.
Recommended video:
07:09The First Derivative Test: Finding Local Extrema
Second Derivative and Its Relation to Concavity
The second derivative of a function provides information about its concavity. If the second derivative is positive, the function is concave up; if negative, it is concave down. In this question, since we are given the graph of the first derivative, we can infer concavity by examining where the first derivative is increasing or decreasing, as these changes indicate the sign of the second derivative.
Recommended video:
06:02The Second Derivative Test: Finding Local Extrema
6:38mWatch next
Master Determining Concavity from the Graph of f with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice