Here are the essential concepts you must grasp in order to answer the question correctly.
Continuity of Functions
A function is continuous at a point if the limit of the function as it approaches that point from both sides equals the function's value at that point. For piecewise functions, this often involves ensuring that the left-hand limit and right-hand limit at the point of interest are equal to the function's value at that point.
Recommended video:
Piecewise Functions
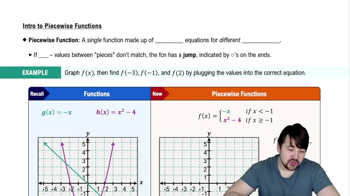
Piecewise functions are defined by different expressions based on the input value. In this case, the function g(x) has three different definitions depending on whether x is less than, equal to, or greater than 1. Understanding how to evaluate these expressions is crucial for analyzing the function's behavior at specific points.
Recommended video:
Limits
Limits describe the behavior of a function as it approaches a certain point. In the context of continuity, we need to evaluate the left-hand limit (as x approaches 1 from the left) and the right-hand limit (as x approaches 1 from the right) to determine if they are equal and match the function's value at that point, which is essential for ensuring continuity.
Recommended video:
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: