Here are the essential concepts you must grasp in order to answer the question correctly.
Continuity of Functions
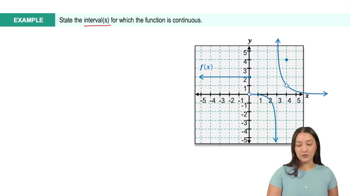
A function is continuous at a point if the limit of the function as it approaches that point equals the function's value at that point. For a function to be continuous over an interval, it must be continuous at every point within that interval. This concept is crucial for determining where a function does not have breaks, jumps, or asymptotes.
Recommended video:
Identifying Discontinuities
Discontinuities can occur due to points where the function is undefined, such as division by zero, or where the left-hand limit and right-hand limit do not match. In the given function, h(x) = 2x / (x^3 - 25x), we need to find values of x that make the denominator zero, as these will indicate potential points of discontinuity.
Recommended video:
Intro to Continuity Example 1
Endpoints and One-Sided Limits
When analyzing continuity at finite endpoints of an interval, it is important to consider one-sided limits. A function can be left-continuous or right-continuous at an endpoint, meaning it approaches the endpoint from the left or right, respectively. This distinction is essential for accurately describing the behavior of the function at the boundaries of its domain.
Recommended video:
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: