[Technology Exercise] Graph the functions in Exercises 113 and 114. Then answer the following questions.
a. How does the graph behave as x → 0⁺?
Give reasons for your answers.
y = (3/2)(x − (1 / x))²/³
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: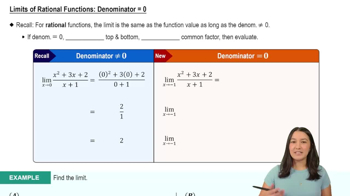



 6:47m
6:47mMaster Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick
Start learning