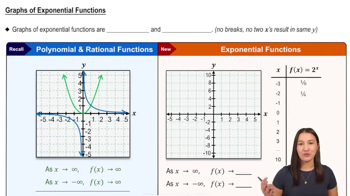
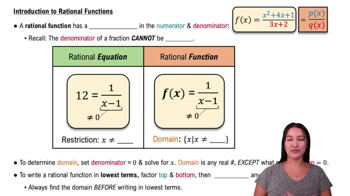
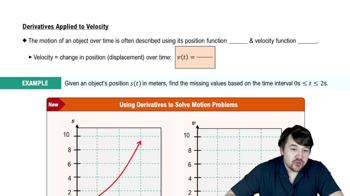
Formal Definitions of One-Sided Limits
Greatest integer function Find (a) limx→400+ ⌊x⌋ and (b) limx→400− ⌊x⌋; then use limit definitions to verify your findings. (c) Based on your conclusions in parts (a) and (b), can you say anything about limx→400 ⌊x⌋? Give reasons for your answer.