Estimating Limits
[Technology Exercise] You will find a graphing calculator useful for Exercises 67–74.
Let g(θ) = (sinθ) / θ.
b. Support your conclusion in part (a) by graphing g near θ₀ = 0.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: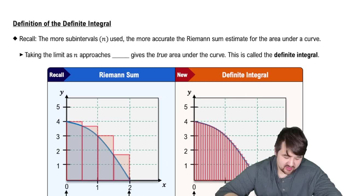


 6:47m
6:47mMaster Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick
Start learning