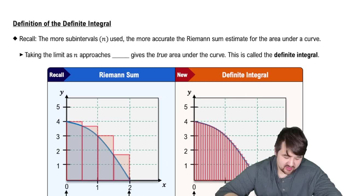
Estimating Limits
[Technology Exercise] You will find a graphing calculator useful for Exercises 67–74.
Let f(x)=(x² − 1)/(|x| − 1).
b. Support your conclusion in part (a) by graphing f near c = -1 and using Zoom and Trace to estimate y-values on the graph as x→−1.