Here are the essential concepts you must grasp in order to answer the question correctly.
Limit of a Function
The limit of a function describes the behavior of the function as the input approaches a certain value. In this case, lim x→a f(x) = L means that as x gets closer to a, the function f(x) approaches the value L. Understanding limits is crucial for analyzing continuity and the behavior of functions near specific points.
Recommended video:
Limits of Rational Functions: Denominator = 0
Delta-Epsilon Definition of a Limit
The delta-epsilon definition formalizes the concept of limits. It states that for every ε (epsilon) greater than 0, there exists a δ (delta) such that if |x - a| < δ, then |f(x) - L| < ε. This definition is essential for proving the validity of limits and understanding the precise conditions under which a function approaches a limit.
Recommended video:
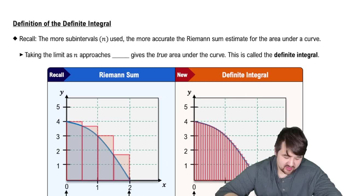
Definition of the Definite Integral
Inequalities and Intervals
Inequalities are used to describe the range of values that a variable can take. The statement |x - a| < δ implies that x lies within the interval (a - δ, a + δ). Understanding how to manipulate and interpret these inequalities is vital for analyzing the behavior of functions in the context of limits and continuity.
Recommended video:
Finding the Domain and Range of a Graph
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: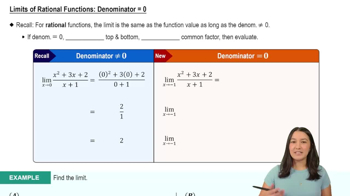


 6:47m
6:47m