Here are the essential concepts you must grasp in order to answer the question correctly.
Secant Line
A secant line is a straight line that intersects a curve at two or more points. In calculus, it is often used to approximate the slope of the curve between those points. The slope of the secant line can be calculated using the formula (f(b) - f(a)) / (b - a), where a and b are the x-coordinates of the points on the curve.
Recommended video:
Slope of a Function
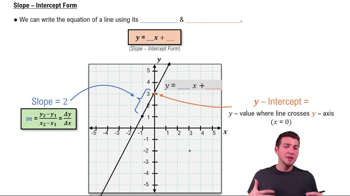
The slope of a function at a given point represents the rate of change of the function's value with respect to changes in its input. For a secant line, the slope is determined by the difference in the function's values at two points divided by the difference in their x-coordinates. This concept is foundational for understanding derivatives, which represent instantaneous rates of change.
Recommended video:
Cube Root Function
The cube root function, denoted as f(x) = x^(1/3), is a mathematical function that returns the number whose cube is x. This function is defined for all real numbers and has a characteristic shape, being continuous and increasing. Understanding its behavior, especially near the origin, is crucial for analyzing the secant line's slope as h approaches zero from both positive and negative directions.
Recommended video:
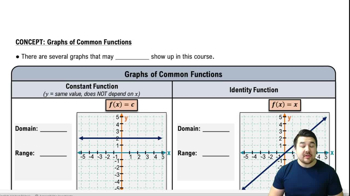
Graphs of Common Functions
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 6:47m
6:47m