Table of contents

0. Functions7h 52m
1. Limits and Continuity2h 2m
2. Intro to Derivatives1h 33m
3. Techniques of Differentiation3h 18m
4. Applications of Derivatives2h 38m
5. Graphical Applications of Derivatives6h 2m
6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
7. Antiderivatives & Indefinite Integrals1h 26m
8. Definite Integrals4h 44m
9. Graphical Applications of Integrals2h 27m
- Area Between Curves
  1h 18m
- Introduction to Volume & Disk Method
  1h 8m
10. Physics Applications of Integrals 3h 16m
- Kinematics
  1h 13m
- Work
  2h 3m
11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 34m
12. Techniques of Integration7h 39m
13. Intro to Differential Equations2h 55m
14. Sequences & Series5h 36m
15. Power Series2h 19m
- Introduction to Power Series
  1h 9m
- Taylor Series & Taylor Polynomials
  1h 10m
16. Parametric Equations & Polar Coordinates7h 58m

1. Limits and Continuity

Introduction to Limits

Calculus

1. Limits and Continuity

Introduction to Limits

Previous problemNext problem

2:44 minutes

Problem 2.6.91

Textbook Question

Using the Formal Definitions

Use the formal definitions of limits as x → ±∞ to establish the limits in Exercises 91 and 92.

If f has the constant value f(x) = k, then lim x → ∞ f(x) = k.

Verified step by step guidance

Step 1: Understand the formal definition of a limit as x approaches infinity. The limit of a function f(x) as x approaches infinity is the value that f(x) gets closer to as x becomes very large.

Step 2: Recognize that if f(x) is a constant function, meaning f(x) = k for all x, then as x approaches infinity, f(x) remains constant at k.

Step 3: Apply the formal definition of limits. For any ε > 0, there exists a number N such that for all x > N, the absolute difference |f(x) - k| is less than ε.

Step 4: Since f(x) = k for all x, the absolute difference |f(x) - k| is 0, which is always less than any positive ε. Therefore, the condition of the limit definition is satisfied.

Step 5: Conclude that the limit of f(x) as x approaches infinity is k, because the function value does not change and remains equal to k for all x.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Limit of a Function

The limit of a function describes the behavior of that function as the input approaches a certain value. In the context of limits as x approaches infinity, it examines how the function behaves as x grows larger and larger. Understanding limits is fundamental in calculus, as it lays the groundwork for concepts such as continuity, derivatives, and integrals.

Formal Definition of a Limit

The formal definition of a limit, often expressed using epsilon-delta notation, provides a rigorous way to define what it means for a function to approach a certain value as the input approaches a specific point. For limits at infinity, this definition helps establish that for every small positive number (epsilon), there exists a corresponding value of x (N) such that for all x greater than N, the function's value is within epsilon of the limit.

Constant Function Limits

A constant function is one where the output value remains the same regardless of the input, expressed as f(x) = k. The limit of a constant function as x approaches infinity is simply the constant value itself, lim x → ∞ f(x) = k. This concept is crucial for understanding how functions behave at extreme values and simplifies the analysis of limits in calculus.

Watch next

Master Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

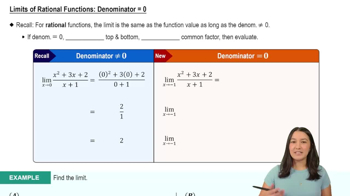
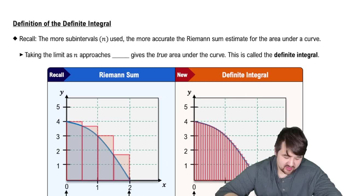
In Exercises 77–80, find a function that satisfies the given conditions and sketch its graph. (The answers here are not unique. Any function that satisfies the conditions is acceptable. Feel free to use formulas defined in pieces if that will help.)

lim x → ±∞ k(x) = 1, lim x → 1⁻ k(x) = ∞, and lim x → 1⁺ k(x) = −∞

Textbook Question

Finding Limits of Differences When x → ±∞

Find the limits in Exercises 84–90. (Hint: Try multiplying and dividing by the conjugate.)

lim x → ∞ (√(x + 9) − √(x + 4))

Textbook Question

Finding Limits of Differences When x → ±∞

Find the limits in Exercises 84–90. (Hint: Try multiplying and dividing by the conjugate.)

lim x → −∞ (√(x² + 3) + x)

Textbook Question

Finding Limits of Differences When x → ±∞

Find the limits in Exercises 84–90. (Hint: Try multiplying and dividing by the conjugate.)

lim x → ∞ (√(9x² − x) − 3x)

Textbook Question

Use formal definitions to prove the limit statements in Exercises 93–96.

lim x → 0 (1 / |x|) = ∞

Textbook Question

Use formal definitions to prove the limit statements in Exercises 93–96.

lim x → −5 (1 / (x + 5)²) = ∞

Textbook Question

Slope of a Curve at a Point

In Exercises 7–18, use the method in Example 3 to find (a) the slope of the curve at the given point P, and (b) an equation of the tangent line at P.

y=√7−x, P(−2,3)

Textbook Question

Finding Limits

In Exercises 3–8, find the limit of each function (a) as x → ∞ and (b) as x → −∞. (You may wish to visualize your answer with a graphing calculator or computer.)

f(x) = 2/x − 3

Show more practices

Download the Mobile app

Privacy

Do not sell my personal information

Accessibility

Patent notice

Sitemap

Using the Formal DefinitionsUse the formal definitions of limits as x → ±∞ to establish the limits in Exercises 91 and 92.If f has the constant value f(x) = k, then lim x → ∞ f(x) = k.

Key Concepts

Limit of a Function

Formal Definition of a Limit

Constant Function Limits

Watch next

Using the Formal Definitions

Use the formal definitions of limits as x → ±∞ to establish the limits in Exercises 91 and 92.

If f has the constant value f(x) = k, then lim x → ∞ f(x) = k.