Use the graph of the greatest integer function y = ⌊x⌋, Figure 1.10 in Section 1.1, to help you find the limits in Exercises 21 and 22.
<IMAGE>
b. limt→4−(t−⌊t⌋)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: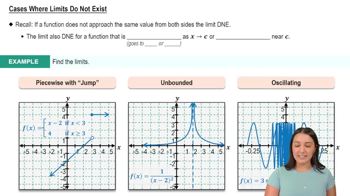


 6:47m
6:47mMaster Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick
Start learning