Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
Limits are fundamental in calculus, representing the value that a function approaches as the input approaches a certain point. In this context, we are interested in the behavior of the function as x approaches infinity, which helps us understand the end behavior of the function and how it simplifies under such conditions.
Recommended video:
Conjugates
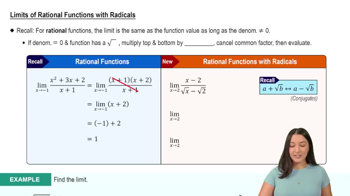
The conjugate of a binomial expression is formed by changing the sign between two terms. In the context of limits, multiplying by the conjugate can help eliminate square roots or simplify expressions, making it easier to evaluate the limit. This technique is particularly useful when dealing with differences of square roots.
Recommended video:
Limits of Rational Functions with Radicals
Rationalization
Rationalization is a method used to eliminate radicals from the denominator or simplify expressions involving square roots. By multiplying the numerator and denominator by the conjugate, we can transform the expression into a more manageable form, allowing for easier calculation of limits, especially as x approaches infinity.
Recommended video:
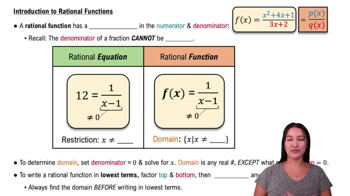
Intro to Rational Functions
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 6:47m
6:47m