6. You are planning to close off a corner of the first quadrant with a line segment 20 units long running from (a, 0) to (0,b). Show that the area of the triangle enclosed by the segment is largest when a = b.
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
5. Graphical Applications of Derivatives
Applied Optimization
Problem 4.5.20a
Textbook Question
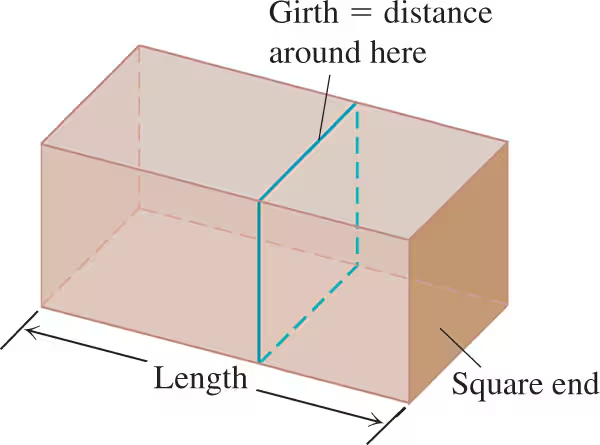
20.The U.S. Postal Service will accept a box for domestic shipment only if the sum of its length and girth (distance around) does not exceed 108 in. a.What dimensions will give a box with a square end the largest possible volume?
 Verified step by step guidance
Verified step by step guidance1
Step 1: Define the variables. Let the side length of the square end be 'x' (in inches), and the length of the box be 'L' (in inches). The girth is the perimeter of the square end, which is 4x.
Step 2: Write the constraint equation. The sum of the length and girth must not exceed 108 inches. Therefore, the constraint is: L + 4x ≤ 108.
Step 3: Express the volume of the box. The volume of the box is given by the area of the square end multiplied by the length: V = x² * L.
Step 4: Solve for 'L' using the constraint equation. From the constraint, L = 108 - 4x. Substitute this into the volume equation to express volume in terms of 'x': V = x² * (108 - 4x).
Step 5: Maximize the volume. To find the dimensions that give the largest possible volume, take the derivative of V with respect to 'x', set it equal to zero, and solve for 'x'. Then, use the constraint equation to find the corresponding 'L'.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Volume of a Box
The volume of a box is calculated by multiplying its length by its width and height. In this case, since the box has a square end, if we denote the side length of the square as 'x' and the length as 'L', the volume can be expressed as V = x^2 * L. Understanding how to express volume in terms of the box's dimensions is crucial for maximizing it under given constraints.
Recommended video:
Finding Volume Using Disks
Girth Calculation
Girth is defined as the distance around the box, specifically calculated as 2 times the width plus 2 times the height. For a box with a square end, this simplifies to G = 4x + 2L. The problem states that the sum of the length and girth must not exceed 108 inches, which provides a constraint that must be satisfied when determining the optimal dimensions for maximum volume.
Recommended video:

Determining Error and Relative Error Example 1
Optimization in Calculus
Optimization involves finding the maximum or minimum values of a function subject to certain constraints. In this scenario, we need to maximize the volume function V = x^2 * L while adhering to the constraint given by the girth equation. Techniques such as substitution and taking derivatives to find critical points will be essential in solving this problem effectively.
Recommended video:

Intro to Applied Optimization: Maximizing Area

 1:13m
1:13mWatch next
Master Intro to Applied Optimization: Maximizing Area with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
