26. Constructing cylinders Compare the answers to the following two construction problems.
a. A rectangular sheet of perimeter 36 cm and dimensions x cm by y cm is to be rolled into a cylinder as shown in part (a) of the figure. What values of x and y give the largest volume?
b. The same sheet is to be revolved about one of the sides of length y to sweep out the cylinder as shown in part (b) of the figure. What values of x and y give the largest volume?

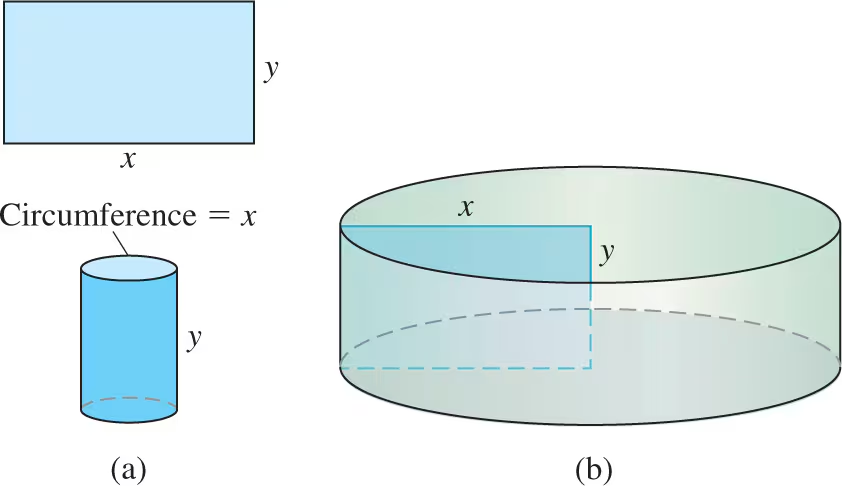
[Technology Exercise] 17. Designing a suitcase A 24-in.-by-36-in. sheet of cardboard is folded in half to form a 24-in.-by-18-in. rectangle as shown in the accompanying figure. Then four congruent squares of side length x are cut from the corners of the folded rectangle. The sheet is unfolded, and the six tabs are folded up to form a box with sides and a lid.

" style="" width="400">

b. Find the domain of V for the problem situation and graph V over this domain.

20.The U.S. Postal Service will accept a box for domestic shipment only if the sum of its length and girth (distance around) does not exceed 108 in. a.What dimensions will give a box with a square end the largest possible volume?

" style="" width="250">

22. A window is in the form of a rectangle surmounted by a semicircle. The rectangle is of clear glass, whereas the semicircle is of tinted glass that transmits only half as much light per unit area as clear glass does. The total perimeter is fixed. Find the proportions of the window that will admit the most light. Neglect the thickness of the frame.

" style="" width="180">

25. Paper folding A rectangular sheet of 8.5-in.-by-11-in. paper is placed on a flat surface. One of the corners is placed on the opposite longer edge, as shown in the figure, and held there as the paper is smoothed flat. The problem is to make the length of the crease as small as possible. Call the length L. Try it with paper.

" style="" width="370">

a. Show that L^2=2x^3/(2x-8.5).

Business and Economics

62. Production level Suppose that c(x)=x^3-20x^2 + 20,000x is the cost of manufacturing x items. Find a production level that will minimize the average cost of making x items.

A cone is formed from a circular piece of material of radius 1 meter by removing a section of angle θ and then joining the two straight edges. Determine the largest possible volume for the cone.

The 8-ft wall shown here stands 27 ft from the building. Find the length of the shortest straight beam that will reach to the side of the building from the ground outside the wall.

The intensity of illumination at any point from a light source is proportional to the square of the reciprocal of the distance between the point and the light source. Two lights, one having an intensity eight times that of the other, are 6 m apart. How far from the stronger light is the total illumination least?