Graphing
In Exercises 69–76, graph each function not by plotting points, but by starting with the graph of one of the standard functions presented in Figures 1.14–1.17 and applying an appropriate transformation.
y = (−2x)²/³
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: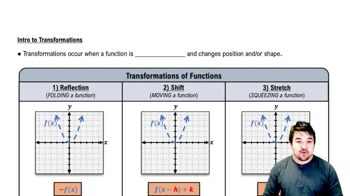

 5:25m
5:25mMaster Intro to Transformations with a bite sized video explanation from Patrick
Start learning