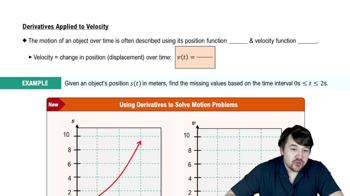
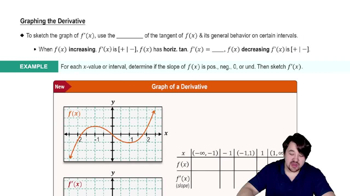
{Use of Tech} Special curves The following classical curves have been studied by generations of mathematicians. Use analytical methods (including implicit differentiation) and a graphing utility to graph the curves. Include as much detail as possible.
y = 8/(x² + 4) (Witch of Agnesi)