{Use of Tech} Elliptic curves The equation y² = x³ - ax + 3, where a is a parameter, defines a well-known family of elliptic curves.
c. By experimentation, determine the approximate value of a (3 < a < 4)at which the graph separates into two curves.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: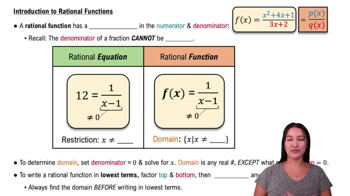

 11:41m
11:41mMaster Summary of Curve Sketching with a bite sized video explanation from Patrick
Start learning