Identifying Extrema
In Exercises 15–18:
a. Find the open intervals on which the function is increasing and those on which it is decreasing.
b. Identify the function’s local and absolute extreme values, if any, saying where they occur.
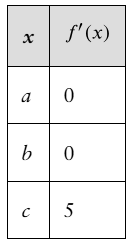
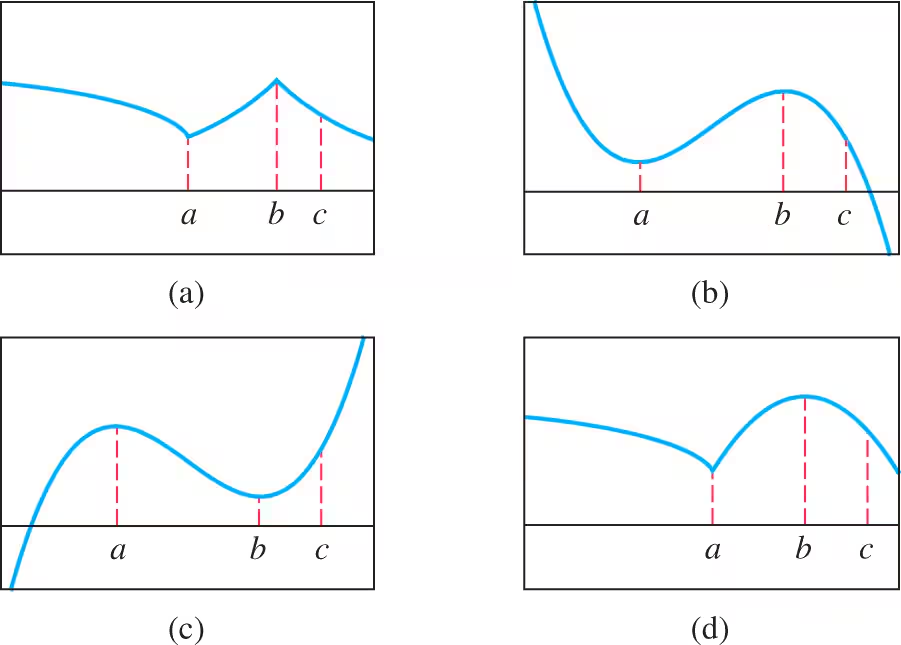
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 5:58m
5:58mMaster Finding Extrema Graphically with a bite sized video explanation from Patrick
Start learning