110. Suppose the derivative of the function y = f(x) is
y'=(x-1)^22(x-2)(x-4).
At what points, if any, does the graph of f have a local minimum, local maximum, or
point of inflection?
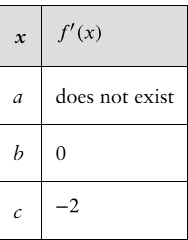
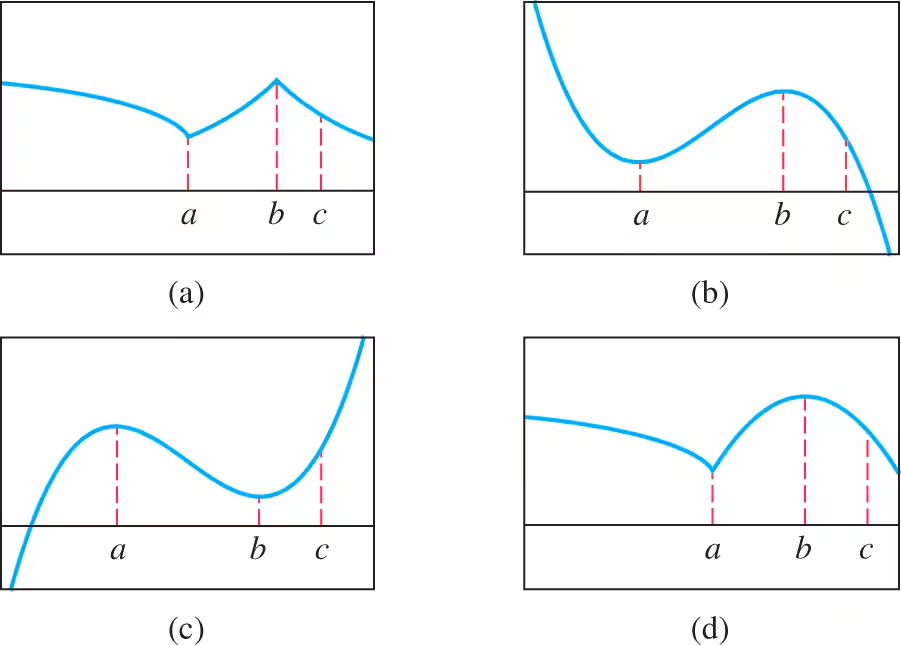
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 5:58m
5:58mMaster Finding Extrema Graphically with a bite sized video explanation from Patrick
Start learning