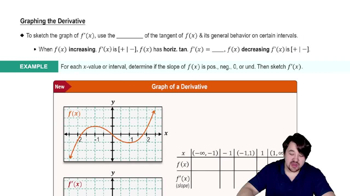
Shifting Graphs
The accompanying figure shows the graph of y = −x² shifted to four new positions. Write an equation for each new graph.
<IMAGE>
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 5:25m
5:25mMaster Intro to Transformations with a bite sized video explanation from Patrick
Start learning