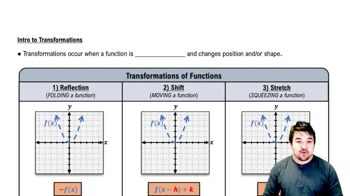
Shifting Graphs
Exercises 27–36 tell how many units and in what directions the graphs of the given equations are to be shifted. Give an equation for the shifted graph. Then sketch the original and shifted graphs together, labeling each graph with its equation.
y = −√x Right 3