Find the inverse function (on the given interval, if specified) and graph both and on the same set of axes. Check your work by looking for the required symmetry in the graphs.
, for
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: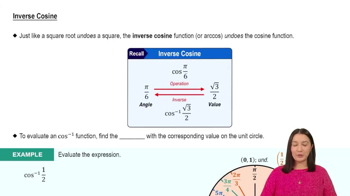



 5:57m
5:57mMaster Graphs of Common Functions with a bite sized video explanation from Patrick
Start learning