Find the inverse of each function (on the given interval, if specified).
, for
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: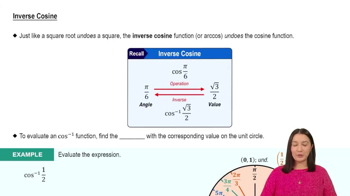



 5:57m
5:57mMaster Graphs of Common Functions with a bite sized video explanation from Patrick
Start learning