Currents in dc transmission lines can be 100 A or higher. Some people are concerned that the electromagnetic fields from such lines near their homes could pose health dangers. For a line that has current 150 A and a height of 8.0 m above the ground, what magnetic field does the line produce at ground level? Express your answer in teslas and as a percentage of the earth's magnetic field, which is 0.50 G. Is this value cause for worry?

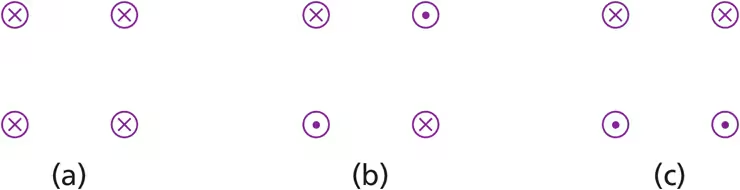
Four long, parallel power lines each carry 100 A currents. A cross-sectional diagram of these lines is a square, 20.0 cm on each side. For each of the three cases shown in Fig. E28.25, calculate the magnetic field at the center of the square.

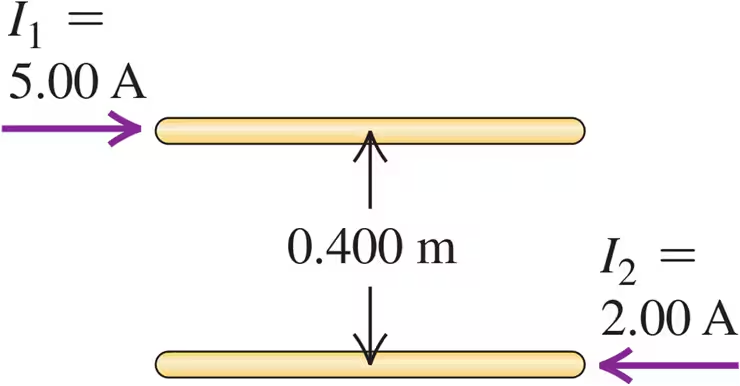
Two long, parallel wires are separated by a distance of 0.400 m (Fig. E28.29). The currents I₁ and I₂ have the directions shown. Calculate the magnitude of the force exerted by each wire on a 1.20-m length of the other. Is the force attractive or repulsive?

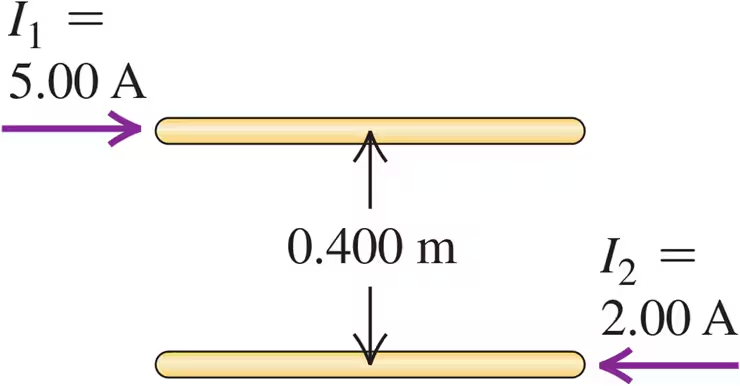
Two long, parallel wires are separated by a distance of 0.400 m (Fig. E28.29). The currents I₁ and I₂ have the directions shown. Each current is doubled, so that I₁ becomes 10.0 A and I₂ becomes 4.00 A. Now what is the magnitude of the force that each wire exerts on a 1.20 m length of the other?

A closed curve encircles several conductors. The line integral $\oint B\cdot dl$ around this curve is $3.83\times {10}^{-4}\text{ T m}$. If you were to integrate around the curve in the opposite direction, what would be the value of the line integral? Explain.

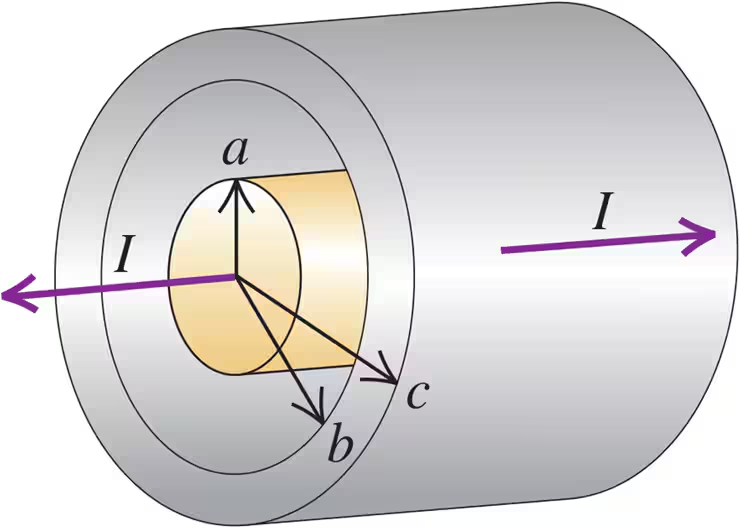
A solid conductor with radius a is supported by insulating disks on the axis of a conducting tube with inner radius b and outer radius c (Fig. E28.43). The central conductor and tube carry equal currents I in opposite directions. The currents are distributed uniformly over the cross sections of each conductor. Derive an expression for the magnitude of the magnetic field at points outside the tube (r > c).

As a new electrical technician, you are designing a large solenoid to produce a uniform 0.150 T magnetic field near the center of the solenoid. You have enough wire for 4000 circular turns. This solenoid must be 55.0 cm long and 2.80 cm in diameter. What current will you need to produce the necessary field?

A 15.0 cm long solenoid with radius 0.750 cm is closely wound with 600 turns of wire. The current in the windings is 8.00 A. Compute the magnetic field at a point near the center of the solenoid.

A solenoid is designed to produce a magnetic field of 0.0270 T at its center. It has radius 1.40 cm and length 40.0 cm, and the wire can carry a maximum current of 12.0 A. What minimum number of turns per unit length must the solenoid have?

A solenoid is designed to produce a magnetic field of 0.0270 T at its center. It has radius 1.40 cm and length 40.0 cm, and the wire can carry a maximum current of 12.0 A. What total length of wire is required?