Back
BackProblem 1a
Two -N weights are suspended at opposite ends of a rope that passes over a light, frictionless pulley. The pulley is attached to a chain from the ceiling. What is the tension in the rope?
Problem 1b
Two -N weights are suspended at opposite ends of a rope that passes over a light, frictionless pulley. The pulley is attached to a chain from the ceiling. What is the tension in the chain?
Problem 3b
A -kg wrecking ball hangs from a uniform, heavy-duty chain of mass kg. What is the tension at a point three-fourths of the way up from the bottom of the chain?
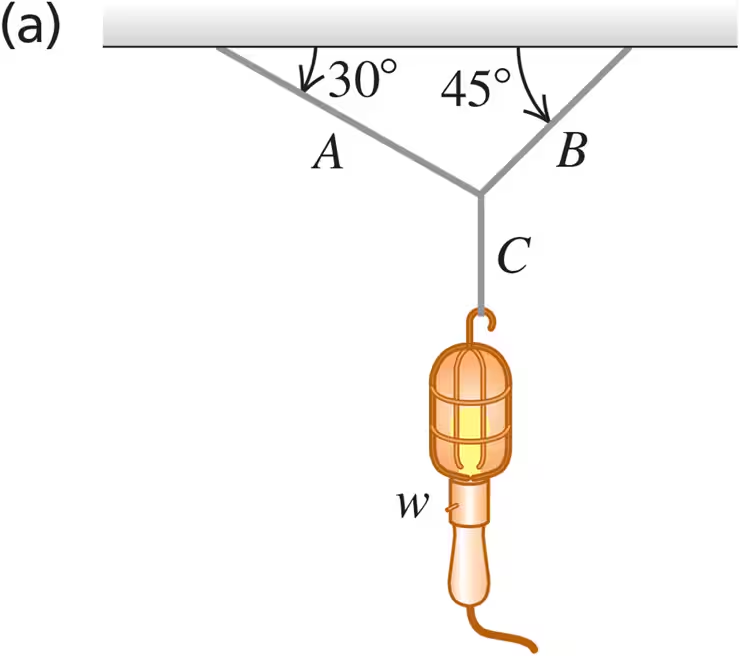
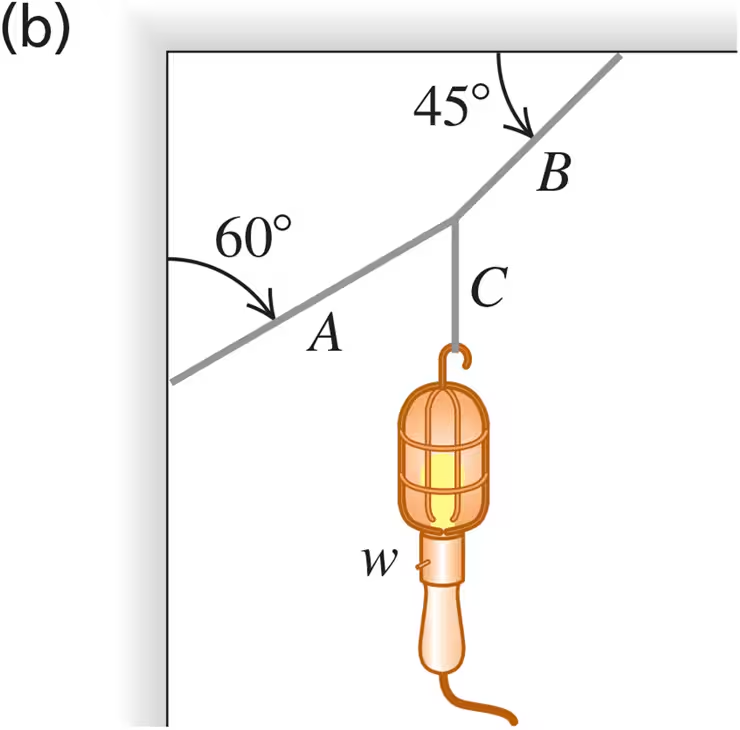
Problem 5a
A picture frame hung against a wall is suspended by two wires attached to its upper corners. If the two wires make the same angle with the vertical, what must this angle be if the tension in each wire is equal to of the weight of the frame? (Ignore any friction between the wall and the picture frame.)
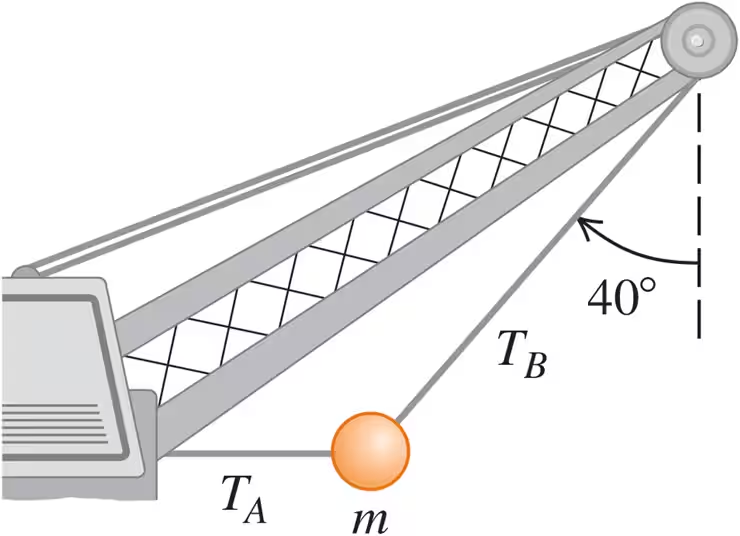
Problem 6
A large wrecking ball is held in place by two light steel cables (Fig. E). If the mass m of the wrecking ball is kg, what are the (a) tension in the cable that makes an angle of with the vertical and (b) the tension in the horizontal cable?
Problem 7
Find the tension in each cord in Fig. E if the weight of the suspended object is .
Problem 9a
A man pushes on a piano with mass kg; it slides at constant velocity down a ramp that is inclined at above the horizontal floor. Neglect any friction acting on the piano. Calculate the magnitude of the force applied by the man if he pushes parallel to the incline.
Problem 9b
A man pushes on a piano with mass kg; it slides at constant velocity down a ramp that is inclined at above the horizontal floor. Neglect any friction acting on the piano. Calculate the magnitude of the force applied by the man if he pushes parallel to the floor.
Problem 10a
A -N physics student stands on a bathroom scale in an elevator that is supported by a cable. The combined mass of student plus elevator is kg. As the elevator starts moving, the scale reads N. Find the acceleration of the elevator (magnitude and direction).
Problem 11a
An astronaut is inside a kg rocket that is blasting off vertically from the launch pad. You want this rocket to reach the speed of sound ( m/s) as quickly as possible, but astronauts are in danger of blacking out at an acceleration greater than . What is the maximum initial thrust this rocket's engines can have but just barely avoid blackout? Start with a free-body diagram of the rocket.
Problem 11b
An astronaut is inside a kg rocket that is blasting off vertically from the launch pad. You want this rocket to reach the speed of sound ( m/s) as quickly as possible, but astronauts are in danger of blacking out at an acceleration greater than . What force, in terms of the astronaut's weight , does the rocket exert on her? Start with a free-body diagram of the astronaut.
Problem 13a
On September 8, 2004, the Genesis spacecraft crashed in the Utah desert because its parachute did not open. The -kg capsule hit the ground at km/h and penetrated the soil to a depth of cm. What was its acceleration (in m/s2 and in g's), assumed to be constant, during the crash?
Problem 13b
On September 8, 2004, the Genesis spacecraft crashed in the Utah desert because its parachute did not open. The -kg capsule hit the ground at km/h and penetrated the soil to a depth of cm. What force did the ground exert on the capsule during the crash? Express the force in newtons and as a multiple of the capsule's weight.
Problem 14a
Three sleds are being pulled horizontally on frictionless horizontal ice using horizontal ropes (Fig. E). The pull is of magnitude N. Find the acceleration of the system.
Problem 14b
Three sleds are being pulled horizontally on frictionless horizontal ice using horizontal ropes (Fig. E). The pull is of magnitude N. Find the tension in ropes and .
Problem 16a
An -kg block of ice, released from rest at the top of a -m-long frictionless ramp, slides downhill, reaching a speed of m/s at the bottom. What is the angle between the ramp and the horizontal?
Problem 16b
An -kg block of ice, released from rest at the top of a -m-long frictionless ramp, slides downhill, reaching a speed of m/s at the bottom. What would be the speed of the ice at the bottom if the motion were opposed by a constant friction force of N parallel to the surface of the ramp?
Problem 17a
A light rope is attached to a block with mass kg that rests on a frictionless, horizontal surface. The horizontal rope passes over a frictionless, massless pulley, and a block with mass is suspended from the other end. When the blocks are released, the tension in the rope is N. Draw two free-body diagrams: one for each block.
Problem 17b
A light rope is attached to a block with mass kg that rests on a frictionless, horizontal surface. The horizontal rope passes over a frictionless, massless pulley, and a block with mass is suspended from the other end. When the blocks are released, the tension in the rope is N. What is the acceleration of either block?
Problem 17c
A light rope is attached to a block with mass kg that rests on a frictionless, horizontal surface. The horizontal rope passes over a frictionless, massless pulley, and a block with mass m is suspended from the other end. When the blocks are released, the tension in the rope is N. Find .
Problem 17d
A light rope is attached to a block with mass kg that rests on a frictionless, horizontal surface. The horizontal rope passes over a frictionless, massless pulley, and a block with mass is suspended from the other end. When the blocks are released, the tension in the rope is N. How does the tension compare to the weight of the hanging block?
Problem 19a
When jumping straight up from a crouched position, an average person can reach a maximum height of about cm. During the jump, the person's body from the knees up typically rises a distance of around cm. To keep the calculations simple and yet get a reasonable result, assume that the entire body rises this much during the jump. With what initial speed does the person leave the ground to reach a height of cm?
Problem 19b
When jumping straight up from a crouched position, an average person can reach a maximum height of about cm. During the jump, the person's body from the knees up typically rises a distance of around cm. To keep the calculations simple and yet get a reasonable result, assume that the entire body rises this much during the jump. Draw a free-body diagram of the person during the jump.
Problem 19c
When jumping straight up from a crouched position, an average person can reach a maximum height of about cm. During the jump, the person's body from the knees up typically rises a distance of around cm. To keep the calculations simple and yet get a reasonable result, assume that the entire body rises this much during the jump. In terms of this jumper's weight w, what force does the ground exert on him or her during the jump?